【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为![]() .如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为
.如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为![]() =3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
=3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)用含t的代数式表示:t秒后,点P表示的数为 ,点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.

参考答案:
【答案】(1)-2+3t,8-2t;(2)相遇点表示的数为4;(3)当t=1或3时,PQ=![]() AB;(4)点P在运动过程中,线段MN的长度不发生变化,理由见解析.
AB;(4)点P在运动过程中,线段MN的长度不发生变化,理由见解析.
【解析】
(1)根据题意,可以用含t的代数式表示出点P和点Q;
(2)根据当P、Q两点相遇时,P、Q表示的数相等,可以得到关于t的方程,然后求出t的值,本题得以解决;
(3)根据PQ=![]() AB,可以求得相应的t的值;
AB,可以求得相应的t的值;
(4)根据题意可以表示出点M和点N,从而可以解答本题.
(1)由题意可得,
t秒后,点P表示的数为:-2+3t,点Q表示的数为:8-2t,
故答案为:-2+3,8-2t;
(2)∵当P、Q两点相遇时,P、Q表示的数相等,
∴-2+3t=8-2t,
解得:t=2,
∴当t=2时,P、Q相遇,
此时,-2+3t=-2+3×2=4,
∴相遇点表示的数为4;
(3)∵t秒后,点P表示的数-2+3t,点Q表示的数为8-2t,
∴PQ=|(-2+3t)-(8-2t)|=|5t-10|,
又![]()
∴|5t-10|=5,
解得:t=1或3,
∴当t=1或3时,PQ=![]() AB;
AB;
(4)点P在运动过程中,线段MN的长度不发生变化,
理由如下:∵点M表示的数为: ![]()
点N表示的数为: ![]()
∴MN=![]()
∴点P在运动过程中,线段MN的长度不发生变化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们的生活水平的提高,家用轿车越来越多地进人普通家庭小明家买了一辆小轿车,他连续记录了7天中每天行驶的路程,以50km为标准,多于50km的记为“+”,不足50km的记为“-”,刚好50km的记为“0”,记录数据如下表:
时间
第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程(km)
-6
-12
0
+6
-18
+38
-8
(1)请你估计小明家的小轿车一月(按30天计)行驶多少千米?
(2)若每行驶100km需要汽油8L,汽油每升6.75元,试求小明家一年(按12个月计)的汽油费用是多少元?(L为汽油单位:升)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个分别含有30°,45°角的一副直角三角板.
(1)如图1叠放在一起
若OC恰好平分∠AOB,则∠AOD= 度;
若∠AOC=40°,则∠BOD= 度;
(2)如图2叠放在一起,∠AOD=4∠BOC,试计算∠AOC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A地将一批物品运往B地,再返回A地,图6表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回.请根据图象中的数据回答:
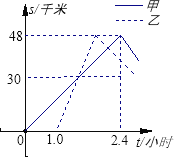
(1)甲车出发多长时间后被乙车追上?
(2)甲车与乙车在距离A地多远处迎面相遇?
(3)甲车从B地返回的速度多大时,才能比乙车先回到A地?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)当a≠0时,求
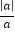 的值.(写出解答过程)
的值.(写出解答过程)(2)若a≠0,b≠0,且
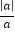 +
+ =0,则
=0,则 的值为 .
的值为 .(3)若ab>0,则
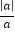 +
+ +
+ 的值为 .
的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在反比例函数
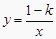 的图象的每一条曲线上,y都随x的增大而增大,则k的值可以是( )
的图象的每一条曲线上,y都随x的增大而增大,则k的值可以是( )
A.-1
B.0
C.1
D.2
相关试题

