搜索
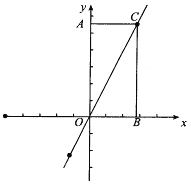
【题目】有一长方形AOBC纸片放在如图所示的坐标系中，且长方形的两边的比为OA：AC＝2：1.
（1）求直线OC的解析式；
（2）求出
＝－5时，函数
的值；
（3）求出＝－5时，自变量的值；
（4）画这个函数的图象；
（5）根据图象回答，当从2减小到－3时，的值是如何变化的？
参考答案：
【答案】（1）
（2）
（3）
略
从4减小到
【解析】分析：
用待定系数法，设点
，根据
的关系即可求出直线
的解析式.
分别把
代入解析式即可.
画出函数图象即可.
通过图象即可得到结论.
详解：设直线的解析式为
，设点，
则
将点代入，
得到
即
代入
解得：
直线的解析式为
当
时，
当
时，
在平面直角坐标系中描出两个点
，连接并延长即可.
如图所示：
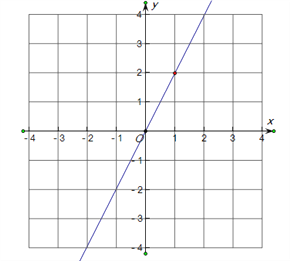
当
从2减小到
时，从4减小到
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列单项式：﹣x，3x2，﹣5x3，7x4，…，﹣37x19，39x20，…，写出第n（n为正整数）个单项式，为解决这个问题，特提供下面的解题思路：
（1）这组单项式的系数的符号规律是 ，系数的绝对值规律是 ；
（2）这组单项式的次数的规律是 ；
（3）根据上面的归纳，可以猜想第n（n为正整数）个单项式吗；
（4）请你根据猜想，写出第2017个、第2018个单项式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知：直线y=
x﹣3分别交x轴于A，交y轴于B，抛物线C1：y=x2+4x+b的顶点D在直线AB上．
（1）求抛物线C1的解析式；
（2）如图2，将抛物线C1的顶点沿射线DA的方向平移得抛物线C2 ， 抛物线C2交y轴于C，顶点为E，若CE⊥AB，求抛物线C2的解析式；
（3）如图3，将直线AB沿y轴正方向平移t（t＞0）个单位得直线l，抛物线C1的顶点在直线AB上平移得抛物线C3 ， 直线l和抛物线C3相交于P、Q，求当t为何值时，PQ=3
？ -
科目： 来源： 题型：
查看答案和解析>>【题目】不等式组
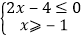的解集是（ ）
A.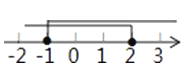
B.
C.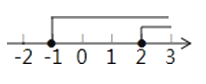
D.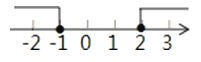
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是某朋的日历表，在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数（如6，7，8，13，14，15，20，21，22），若圈出的9个数中，最大数与最小数的积为192，则这9个数的和为（ ）
A.32
B.126
C.135
D.144 -
科目： 来源： 题型：
查看答案和解析>>【题目】符号“f”表示一种运算，它对一些数的运算如下：f（1）=1+
，f（2）=1+
，f（3）=1+
，f（4）=1+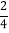
…（1）利用以上运算规律，写出f（2017）=__________；
（2）计算：f（1）f（2）f（3）…f（100）的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】对某市8所学校抽取共1 000名学生进行800米跑达标抽样检测．结果显示该市达标学生人数超过半数，达标率达到52.5%．图l、图2反映的是本次抽样中的具体数据．
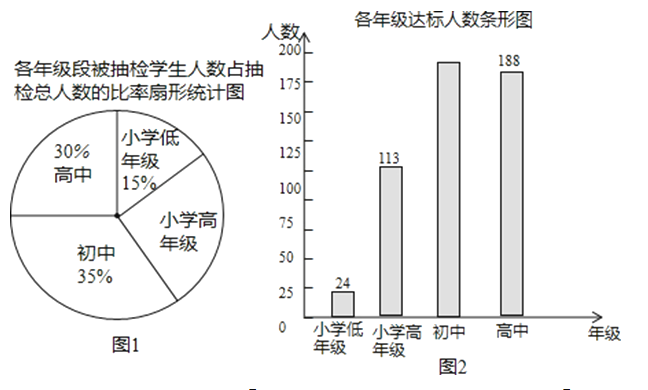
根据以上信息，下列判断：①小学高年级被抽检人数为200人；②小学、初中、高中学生中高中生800米跑达标率最大；③小学生800米跑达标率低于33%；④高中生800米跑达标率超过70%．其中判断正确的有（ ）
A.0个
B.1个
C.2个
D.3个
相关试题
