【题目】观察下列单项式:﹣x,3x2,﹣5x3,7x4,…,﹣37x19,39x20,…,写出第n(n为正整数)个单项式,为解决这个问题,特提供下面的解题思路:
(1)这组单项式的系数的符号规律是 ,系数的绝对值规律是 ;
(2)这组单项式的次数的规律是 ;
(3)根据上面的归纳,可以猜想第n(n为正整数)个单项式吗;
(4)请你根据猜想,写出第2017个、第2018个单项式.
参考答案:
【答案】(1)(﹣1)n;2n﹣1;(2)从1开始的连续自然数;(3)(﹣1)n(2n﹣1)xn;(4)﹣4025x2013;4027x2014;
【解析】
所有式子均为单项式,先观察数字因数,可得规律: ![]() ,再观察字母因数,可得规律为:
,再观察字母因数,可得规律为: ![]() ;然后代入求值即可.
;然后代入求值即可.
(1)根据各项系数的符号以及系数的值得出:
这组单项式的系数的符号规律是(﹣1)n,系数的绝对值规律是2n﹣1.
(2)这组单项式的次数的规律是从1开始的连续自然数.
(3)第n个单项式是:(﹣1)n(2n﹣1)xn.
(4)第2013个单项式是﹣4025x2013,第2014个单项式是4027x2014.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2
 ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图中的图象(折线
 )描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为
 千米/时;
千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习有理数的乘法后,老师给同学们这样一道题目:计算:49
 ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下: 小明:原式=﹣
 ×5=﹣
×5=﹣ =﹣249
=﹣249 ;
; 小军:原式=(49+
 )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+ ×(﹣5)=﹣249
×(﹣5)=﹣249 ;
; (1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19
 ×(﹣8)
×(﹣8) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知:直线y=
 x﹣3分别交x轴于A,交y轴于B,抛物线C1:y=x2+4x+b的顶点D在直线AB上.
x﹣3分别交x轴于A,交y轴于B,抛物线C1:y=x2+4x+b的顶点D在直线AB上.
(1)求抛物线C1的解析式;
(2)如图2,将抛物线C1的顶点沿射线DA的方向平移得抛物线C2 , 抛物线C2交y轴于C,顶点为E,若CE⊥AB,求抛物线C2的解析式;
(3)如图3,将直线AB沿y轴正方向平移t(t>0)个单位得直线l,抛物线C1的顶点在直线AB上平移得抛物线C3 , 直线l和抛物线C3相交于P、Q,求当t为何值时,PQ=3 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
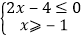 的解集是( )
的解集是( )
A.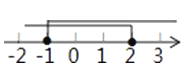
B.
C.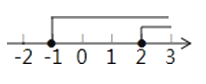
D.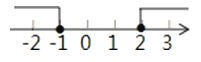
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一长方形AOBC纸片放在如图所示的坐标系中,且长方形的两边的比为OA:AC=2:1.
(1)求直线OC的解析式;
(2)求出
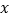 =-5时,函数
=-5时,函数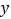 的值;
的值;(3)求出
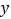 =-5时,自变量
=-5时,自变量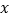 的值;
的值;(4)画这个函数的图象;
(5)根据图象回答,当
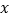 从2减小到-3时,
从2减小到-3时,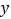 的值是如何变化的?
的值是如何变化的?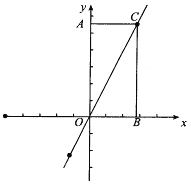
相关试题

