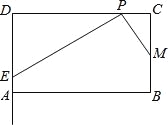
【题目】如图,在矩形ABCD中,AB=m,BC=4,点M为边BC的中点,点P为边CD上的动点(点P异于C,D两点).连接PM,过点P作PM的垂线与射线DA相交于点E(如图).
设CP=x,DE=y.
(1)求y与x之间的函数关系式;
(2)若点P在线段DC上运动时,点E总在线段AD上,求m的取值范围;
(3)当m=8时,是否存在点P,使得点D关于直线PE的对称点F落在边AB上?若存在,求x的值;若不存在,请说明理由.
参考答案:
【答案】(1)、y=﹣![]() x2+
x2+![]() mx;(2)、m≥4
mx;(2)、m≥4![]() ;(3)、x=2﹣
;(3)、x=2﹣![]()
【解析】
试题分析:(1)、由△CPM∽△DEP得![]() =
=![]() 由此即可解决问题.(2)、y=﹣
由此即可解决问题.(2)、y=﹣![]() x2+
x2+![]() mx,根据函数的最大值是4,列出不等式即可解决问题.(3)、存在,过P作PH垂直于AB,由对称的性质得到:PD′=PD=8﹣x,ED′=ED=y=﹣
mx,根据函数的最大值是4,列出不等式即可解决问题.(3)、存在,过P作PH垂直于AB,由对称的性质得到:PD′=PD=8﹣x,ED′=ED=y=﹣![]() x2+4x,EA=AD﹣ED=
x2+4x,EA=AD﹣ED=![]() x2﹣4x+4,∠PD′E=∠D=90°,在Rt△D′PH中,PH=4,D′P=DP=8﹣x,根据勾股定理表示出D′H,再由△ED′A∽△D′PH,由相似得比例,将各自表示出的式子代入,可列出关于x的方程,求出方程的解即可得到满足题意的x的值.
x2﹣4x+4,∠PD′E=∠D=90°,在Rt△D′PH中,PH=4,D′P=DP=8﹣x,根据勾股定理表示出D′H,再由△ED′A∽△D′PH,由相似得比例,将各自表示出的式子代入,可列出关于x的方程,求出方程的解即可得到满足题意的x的值.
试题解析:(1)、∵PE⊥PM,∴∠EPM=90°, ∴∠DPE+∠CPM=90°, 又矩形ABCD,∴∠D=90°,
∴∠DPE+∠DEP=90°, ∴∠CPM=∠DEP,又∠C=∠D=90°, ∴△CPM∽△DEP, ∴![]() =
=![]() ,
,
又CP=x,DE=y,AB=DC=m,∴DP=m﹣x, 又M为BC中点,BC=4,∴CM=2, ∴![]() =
=![]() ,∴y=﹣
,∴y=﹣![]() x2+
x2+![]() mx.
mx.
(2)、由题意:﹣![]() x2+
x2+![]() mx≤4, ∴
mx≤4, ∴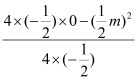 ≤4, ∴m2≥32, ∵m>0 ∴m≥4
≤4, ∴m2≥32, ∵m>0 ∴m≥4![]() .
.
(3)、存在,过P作PH⊥AB于点H,

∵点D关于直线PE的对称点D′落在边AB上, ∴PD′=PD=8﹣x,ED′=ED=y=﹣![]() x2+4x,EA=AD﹣ED=
x2+4x,EA=AD﹣ED=![]() x2﹣4x+4,∠PD′E=∠D=90°, 在Rt△D′PH中,PH=4,D′P=DP=8﹣x,
x2﹣4x+4,∠PD′E=∠D=90°, 在Rt△D′PH中,PH=4,D′P=DP=8﹣x,
根据勾股定理得:D′H=![]() ,
,
∵∠ED′A=180°﹣90°﹣∠PD′H=90°﹣∠PD′H=∠D′PH,∠PD′E=∠PHD′=90°,
∴△ED′A∽△D′PH, ∴ , 整理得:x2﹣4x+2=0,
, 整理得:x2﹣4x+2=0,
解得:x=2±![]() . 当x=2+
. 当x=2+![]() 时,y=5+2
时,y=5+2![]() >4,
>4,
此时,点E在边DA的延长线上,D关于直线PE的对称点不可能落在边AB上,所以舍去.
当x=2﹣![]() 时,y=5﹣2
时,y=5﹣2![]() <4,此时,点E在边AD上,符合题意.
<4,此时,点E在边AD上,符合题意.
所以当x=2﹣![]() 时,点D关于直线PE的对称点D′落在边AB上.
时,点D关于直线PE的对称点D′落在边AB上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b为有理数,若a99b100<0,且a﹣b>0.则下列推断正确的是( )
A. a>0,b>0 B. a>0,b<0 C. a<0,b>0 D. a<0,b<0
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.“打开电视,正在播放新闻联播节目”是必然事件
B.某种彩票中奖概率为10%是指买10张一定有一张中奖
C.了解某种节能灯的使用寿命应采用全面检查
D.一组数据3,5,4,6,7的中位数是5,方差是2 -
科目: 来源: 题型:
查看答案和解析>>【题目】我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下两组勾股数:11、 、 ; 13、 、 ;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别表示为 和 ,请用所学知识说明它们是一组勾股数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)与x轴一个交点在﹣1,﹣2之间,对称轴为直线x=1,图象如图,给出以下结论:①b2﹣4ac>0;②abc>0;③2a﹣b=0;④8a+c<0;⑤a+
 b+
b+ c<0.其中结论正确的个数有( )
c<0.其中结论正确的个数有( )
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
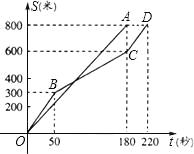
A.小莹的速度随时间的增大而增大
B.小梅的平均速度比小莹的平均速度大
C.在起跑后180秒时,两人相遇
D.在起跑后50秒时,小梅在小莹的前面
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ax2﹣4ay2= .
相关试题

