【题目】如图,抛物线y=![]() x2﹣
x2﹣![]() x+3与x轴交于A,B两点,与y轴交于点C,点M的坐标为(2
x+3与x轴交于A,B两点,与y轴交于点C,点M的坐标为(2![]() , 1).以M为圆心,2为半径作⊙M.则下列说法正确的是________(填序号).
, 1).以M为圆心,2为半径作⊙M.则下列说法正确的是________(填序号).
①tan∠OAC=![]() ;
;
②直线AC是⊙M的切线;
③⊙M过抛物线的顶点;
④点C到⊙M的最远距离为6;
⑤连接MC,MA,则△AOC与△AMC关于直线AC对称.

参考答案:
【答案】①②③④
【解析】试题分析:过点M作MN⊥AB于点N,交⊙M于点D,则AN=BN,

∵抛物线y=![]() x2-
x2-![]() x+3与x轴交于A,B两点,与y轴交于点C,
x+3与x轴交于A,B两点,与y轴交于点C,
∴A,B两点的坐标是(![]() ,0),(3
,0),(3![]() ,0),点C的坐标为(0,3),
,0),点C的坐标为(0,3),
∴OA=![]() ,OC=3,AN=
,OC=3,AN=![]() ,
,
∴tan∠OAC=![]() =
=![]() ,
,
∴①正确,∠CAO=60°,
∵点M的坐标为(2![]() ,1),
,1),
∴MN=1,
∵tan∠MAN=![]() ,
,
∴∠MAN=30°,
∴MA⊥AC,
∴直线AC是⊙M的切线,
∴②正确,
∵⊙M的半径为2,
∴DN=1,
∴D点的坐标为(2![]() ,-1),
,-1),
∵抛物线y=![]() x2-
x2-![]() x+3的顶点坐标为(2
x+3的顶点坐标为(2![]() ,-1),
,-1),
∴⊙M过抛物线的顶点,
∴③正确,
∵OA=![]() ,∠ACO=30°,
,∠ACO=30°,
∴AC=2![]() ,
,
∵MA⊥AC,
∴CM=![]() ,
,
∴点C到⊙M的最远距离为4+2=6,
∴④正确,
∵∠AOC=90°,∠AMC≠90°,
∴△AOC与△AMC关于直线AC不对称,
∴⑤错误,
故答案为:①②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 若AP=BP,则点P是线段的中点 B. 若点C在线段AB上,则AB=AC+BC
C. 若AC+BC>AB,则点C一定在线段AB外 D. 两点之间,线段最短
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中: ①abc<0;②4ac﹣b2>0;③a﹣b+c>2;④a<b<0;⑤ac+2=b,
正确的个数有________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,对于任意的三个点A、B、C,给出如下定义:若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的“三点矩形”.在点A,B,C的所有“三点矩形”中,若存在面积最小的矩形,则称该矩形为点A,B,C的“迷你三点矩形”.
如图1,矩形DEFG,矩形IJCH都是点A,B,C的“三点矩形”,矩形IJCH是点A,B,C的“迷你三点矩形”.
如图2,已知M(4,1),N(-2,3),点P(m,n).
(1)①若m=1,n=4,则点M,N,P的“迷你三点矩形”的周长为 ,面积为 ;
②若m=1,点M,N,P的“迷你三点矩形”的面积为24,求n的值;
(2)若点P在直线y=-2x+4上.当点M,N,P的“迷你三点矩形”为正方形时,直接写出点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )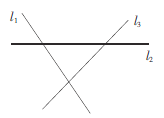
A.一处B.二处C.三处D.四处
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB=BC.如果
 ,那么该数轴的原点O的位置应该在( )
,那么该数轴的原点O的位置应该在( )
A.点A的左边
B.点A与点B之间
C.点B与点C之间(靠近点B)
D.点C的右边
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②3a+c<0,③a﹣b+c>0,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣
 ,y2)在该图象上,则y1>y2,其中正确的结论是 .(填入正确结论的序号)
,y2)在该图象上,则y1>y2,其中正确的结论是 .(填入正确结论的序号)
相关试题

