【题目】如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
(1)写出点B的坐标;
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t,当t为何值时,PQ∥BC;
(3)在Q的运行过程中,当Q运动到什么位置时,使△ADQ的面积为9,求此时Q点的坐标.

参考答案:
【答案】(1)B(8,6)(2)t为![]() (3)当Q运动到距原点3cm位置时,使△ADQ的面积为9,此时Q点的坐标(3,0)或(-3,0)
(3)当Q运动到距原点3cm位置时,使△ADQ的面积为9,此时Q点的坐标(3,0)或(-3,0)
【解析】
试题(1)根据点的特点可以直接写出坐标;
(2)由平行的位置和移动的距离可以设出时间t,从而构成方程解决;
(3)分在D点左右两边两种情况讨论构成的三角形,根据面积求出点的坐标.
试题解析:(1)∵AB=DC=8 AD=BC=6
∴B(8,6)
(2)运动时间为t秒 则t秒时P(3t,6)Q(8-4t,0)
∵PQ ∥BC 且 BC∥ AO
∴PQ∥A0即y轴
∴ 3t=8-4t
∴t=![]()
∴t=![]() 秒时 PQ//BC
秒时 PQ//BC
(3)∵Q在射线CD方向匀速运动.
Q在0点右侧时Q坐标(8-4t,0)
S=![]() AD.DQ
AD.DQ
∴9=![]() ×6(8-4t)
×6(8-4t)
∴t=![]()
此时8-4t=8-4×![]() =3
=3
∴Q(3,0)
Q在点0左侧时Q(8-4t,0) S=![]() AD×DQ 9=
AD×DQ 9=![]() ×6×(4t-8)
×6×(4t-8)
∴t=![]()
此时8-4t=8-4×![]() =-3
=-3
∴Q(-3,0)
∴Q点距原点3个单位时,面积为9
此时Q(3,0)或(-3,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD= ______ °时,四边形BECD是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC .
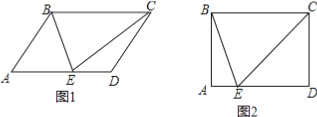
(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
-
科目: 来源: 题型:
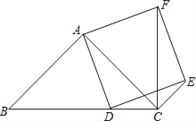
查看答案和解析>>【题目】如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,以AD为边作正方形ADEF,连结CF,CE.
(1)求证:△ABD≌△ACF;
(2)如果BD=AC,求证:CD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
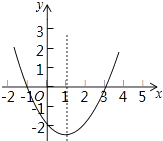
A.函数有最小值
B.当﹣1<x<3时,y>0
C.当x<1时,y随x的增大而减小
D.对称轴是直线x=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC,BD相交于点O,过点O与AD上的一点E作直线OE,交BA的延长线于点F.若AD=4,DC=3,AF=2,则AE的长是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用小立方体搭成一个几何体,从正面和上面看到该几何体的形状图如图所示,搭建这样的几何体最多要几个小立方体?最少要几个小立方体?并画出最多和最少时从左面看到的形状图.

相关试题

