【题目】如图,在ABCD中,对角线AC,BD相交于点O,过点O与AD上的一点E作直线OE,交BA的延长线于点F.若AD=4,DC=3,AF=2,则AE的长是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】C
【解析】解:如图,延长FO,交BC于点G.
∵四边形ABCD是平行四边形,
∴OD=OB,AD∥BC,AB=DC=3,
∴∠EDO=∠GBO,又∠DOE=∠BOG,
∴△DOE≌△BOG(ASA).
∴DE=BG.
∵AE∥BG,
∴△AEF∽△BGF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
设AE=2x,则BG=5x,
∴DE=BG=5x,
∵AE+DE=AD=4,
∴2x+5x=4,
∴x= ![]() ,
,
∴AE=2x= ![]() .
.
故选C.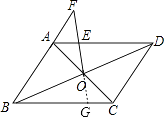
延长FO,交BC于点G.由平行四边形的性质得出OD=OB,AD∥BC,AB=DC=3,根据ASA证明△DOE≌△BOG,得出DE=BG.再由AE∥BG,得出△AEF∽△BGF,根据相似三角形对应边成比例得出 ![]() =
= ![]() =
= ![]() ,设AE=2x,则BG=5x,DE=BG=5x,根据AE+DE=AD=4,求出x=
,设AE=2x,则BG=5x,DE=BG=5x,根据AE+DE=AD=4,求出x= ![]() ,那么AE=2x=
,那么AE=2x= ![]() .
.
-
科目: 来源: 题型:
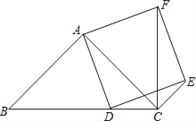
查看答案和解析>>【题目】如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,以AD为边作正方形ADEF,连结CF,CE.
(1)求证:△ABD≌△ACF;
(2)如果BD=AC,求证:CD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
(1)写出点B的坐标;
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t,当t为何值时,PQ∥BC;
(3)在Q的运行过程中,当Q运动到什么位置时,使△ADQ的面积为9,求此时Q点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
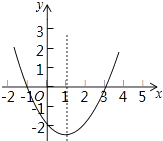
A.函数有最小值
B.当﹣1<x<3时,y>0
C.当x<1时,y随x的增大而减小
D.对称轴是直线x=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】用小立方体搭成一个几何体,从正面和上面看到该几何体的形状图如图所示,搭建这样的几何体最多要几个小立方体?最少要几个小立方体?并画出最多和最少时从左面看到的形状图.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①、②、③、④四个图形都是平面图形,观察图②和表中对应数值,探究计数的方法并解答下面的问题.

(1)数一数每个图各有多少顶点、多少条边、这些边围成多少区域,将结果填入下表:
图形
①
②
③
④
顶点数(V)
边数(E)
区域数(F)
(2)根据表中的数值,写出平面图的顶点数、边数、区域数之间的关系;
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,连接BE,将BE绕点B顺时针旋转90°,得BF,连接AD,BD,AF
(1)如图①,D、E分别在AC,BC边上,求证:四边形ADBF为平行四边形;
(2)△DEC绕点C逆时针旋转,其它条件不变,如图②,(1)的结论是否成立?说明理由.
(3)在图①中,将△DEC绕点C逆时针旋转一周,其它条件不变,问:旋转角为多少度时.四边形ADBF为菱形?直接写出旋转角的度数.

相关试题

