【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC .
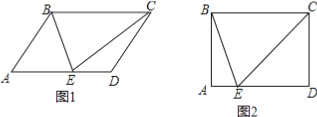
(1)如图1,判断△BCE的形状,并说明理由;
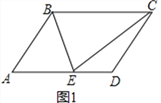
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)结论: ![]() 是等腰三角形,根据平行四边形的性质以及已知条件,只要证明
是等腰三角形,根据平行四边形的性质以及已知条件,只要证明![]() 即可.
即可.
(2)先证明四边形ABCD是矩形,然后分别在![]() 和
和![]() 中利用勾股定理即可解决问题.
中利用勾股定理即可解决问题.
试题解析:(1)如图1中,结论:△BCE是等腰三角形.
证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠CBE=∠AEB,
∵BE平分∠AEC,
∴∠AEB=∠BEC,
∴∠CBE=∠BEC,
∴CB=CE,
∴△CBE是等腰三角形.
(2)如图2中,∵四边形ABCD是平行四边形,∠A=90°,
∴四边形ABCD是矩形,
∴∠A=∠D=90°,BC=AD=5,
在RT△ECD中,∵∠D=90°,ED=AD-AE=4,EC=BC=5,
![]()
在![]() 中,∵∠A=90°AB=3.AE=1,
中,∵∠A=90°AB=3.AE=1,
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴交与点E,已知点B(﹣1,0).
(1)点A的坐标: , 点E的坐标:;
(2)若二次函数y=﹣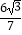 x2+bx+c过点A、E,求此二次函数的解析式;
x2+bx+c过点A、E,求此二次函数的解析式;
(3)P是AC上的一个动点(P与点A、C不重合)连结PB、PD,设l是△PBD的周长,当l取最小值时,求点P的坐标及l的最小值并判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由.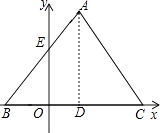
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD= ______ °时,四边形BECD是矩形.

-
科目: 来源: 题型:
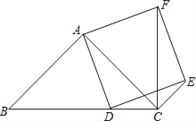
查看答案和解析>>【题目】如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,以AD为边作正方形ADEF,连结CF,CE.
(1)求证:△ABD≌△ACF;
(2)如果BD=AC,求证:CD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
(1)写出点B的坐标;
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t,当t为何值时,PQ∥BC;
(3)在Q的运行过程中,当Q运动到什么位置时,使△ADQ的面积为9,求此时Q点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
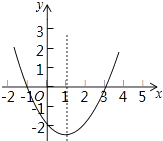
A.函数有最小值
B.当﹣1<x<3时,y>0
C.当x<1时,y随x的增大而减小
D.对称轴是直线x=1
相关试题

