搜索
【题目】在进行二次根式化简时,我们有时会碰上如
,
, 
一样的式子,其实我们还可以将其进一步化简：
=
（一），
（二），
（三），
还可以用以下方法化简： 
=
（四）
以上这种化简的方法叫做分母有理化。
(1)请化简
=___.
(2)若a是
的小数部分则
=___.
(3)矩形的面积为
,一边长为
，则它的周长为___.
(4)化简
.
参考答案：
【答案】(1) 
；(2) 
； (3) 
；(4) 
.
【解析】试题解析：
（1）分子、分母同乘以最简有理化因式
，化简即可；
（2）由题意可得a=
-1，代入分母有理化即可．
（3）首先求另一边长为： 
，化简再按矩形的周长公式解答；
（4）把各加数分母有理化，再加减即可．
试题解析：（1）
，
故答案为： 
；；
（2）∵
＜
＜
，a是
的小数部分，
∴a=
-1，
∴
（3）另一边长为： 
,
周长为：2（17+7
+
-2）=30+16
；
（4）
=
=
=
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某食品厂从生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如下表：
与标准质量的差值
（单位：g）
5
20
1
3
6
袋 数
1
4
3
4
5
3
（1）这批样品的平均质量比标准质量多还是少？多或少几克？
（2）若每袋标准质量为450克，则抽样检测的总质量是多少？
-
科目： 来源： 题型：
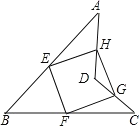
查看答案和解析>>【题目】已知：在平行四边形ABCD中，AE⊥BC，垂足为E，CE=CD，点F为CE的中点，点G为CD上的一点，连接DF，EG，AG，∠1=∠2．
（1）求证：G为CD的中点.
(2) 若CF=2，AE=3，求BE的长；
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，E. F. G、H分别是边AB、BC、CD、DA的中点.
(1)判断四边形EFGH的形状，并说明你的理由；
(2)连接BD和AC,当BD、AC满足何条件时,四边形EFGH是正方形？证明你的理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1)问题发现
如图1,点E.F分别在正方形ABCD的边BC、CD上,∠EAF=45°，连接EF、则EF=BE+DF，试说明理由；
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E.F分别在边BC、CD上,∠EAF=45°，若∠B，∠D都不是直角，则当∠B与∠D满足等量关系 时，仍有EF=BE+DF；
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°，猜想BD、DE、EC满足的等量关系，并写出推理过程。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G为AF的中点，∠ACD=2∠ACB．若DG=3，EC=1，则DE的长为（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读与理解：
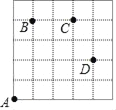
如图，一只甲虫在5×5的方格（每个方格边长均为1）上沿着网格线爬行．若我们规定：在如图网格中，向上（或向右） 爬行记为“+”，向下（或向左） 爬行记为“﹣”，并且第一个数表示左右方向，第二个数表示上下方向．
例如：从A到B记为：A→B（+1，+4），从D到C记为：D→C（﹣1，+2）．
思考与应用：
（1）图中A→C（ ， ），B→C（ ， ），D→A（ ， ）
（2）若甲虫从A到P的行走路线依次为：（+3，+2）→（+1，+3）→（+1，﹣2），请在图中标出P的位置．
（3）若甲虫的行走路线为A→（+1，+4）→（+2，0）→（+1，﹣2）→（﹣4，﹣2），请计算该甲虫走过的总路程．
相关试题
