【题目】某超市购进一批文具袋,每个进价为10元.试销售期间,记录的每天的销售数量与销售单价的数据如下表:
销售单价x(元 | 11 | 12 | 13 | 14 | 15 | … |
销售数量y(个) | 38 | 36 | 34 | 32 | 30 | … |
备注:物价局规定,每个文具袋的售价不低于10元且不高于18元 | ||||||
请你根据表中信息解答下列问题:
(1)y是x的函数,其函数关系式为
(2)营业员发现有一天的利润是150元,则销售单价为元.
(3)试销售的目的是想要每天获得最大的销售利润.请你帮助销售经理计算一下,在这种情况下单价x(元)应定为多少时,每天的销售利润w(元)最大,最大利润是多少元?
参考答案:
【答案】
(1)一次;y=﹣2x+60
(2)15
(3)解:由题意得w=(﹣2x+60)(x﹣10)=﹣2x2+80x﹣600=﹣2(x﹣20)2+200,
∵a=﹣2<0,
∴当x<20时,w随x的增大而增大,
∵10≤x≤18,
∴当x=18时,w最大,最大值为﹣2(18﹣20)2+200=192,
答:文具袋的单价应定为18元时,每天的销售利润w最大,最大利润是192元.
【解析】解:(1.)由表格可知,销售单价每增加1元,其销售数量就减少2件, ∴y是x的一次函数,
设y=kx+b,
将x=11、y=38,x=12、y=36代入,得:![]() ,
,
解得: ![]() ,
,
∴y=﹣2x+60,
所以答案是:一次,y=﹣2x+60;
(2.)根据题意,得:(x﹣10)(﹣2x+60)=150,
整理,得:x2﹣40x+375=0,
解得:x=15或x=25,
∵每个文具袋的售价不低于10元且不高于18元,
∴销售单价x=15,
所以答案是:15;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
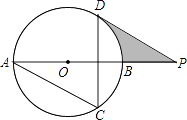
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1,1,系数和为2;(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1,系数和为4;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1,系数和为8……

根据以上规律,解答下列问题:
(1)(a+b)4的展开式共有多少项,系数分别为多少;
(2)写出(a+b)5的展开式;
(3)(a+b)n的展开式共有多少项,系数和为多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五四”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号
进价(元/只)
售价(元/只)
A型
10
12
B型
15
23
(1)设购进A型文具x只,销售利润为w元,求w与x的函数关系式?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一张如图①所示的长方形铁皮四个角都剪去边长为30cm的正方形,再四周折起,做成一个有底无盖的铁盒,如图②.铁盒底面长方形的长是4acm,宽是3acm.

(1)请用含有a的代数式表示图①中原长方形铁皮的面积;
(2)若要在铁盒的外表面涂上某种油漆,每1元钱可涂油漆的面积为
 cm2,则在这个铁盒的外表面涂上油漆需要多少钱(用含有a的代数式表示)?
cm2,则在这个铁盒的外表面涂上油漆需要多少钱(用含有a的代数式表示)? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC=2,∠A=90°,将一块与△ABC全等的三角板的直角顶点放在点C上,一直角边与BC重叠.
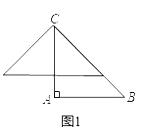
(1)操作1:固定△ABC,将三角板沿C→B方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿C→B方向平移的距离为;
(2)操作2:在(1)的情况下,将三角板BC的中点M顺时针方向旋转角度a(0°<a<90°),如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;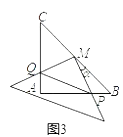
(3)在(2)的情形下,连PQ,则当△MPQ的面积等于四边形MPAQ的面积的一半时,四边形MPAQ的形状为 , 此时BP= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).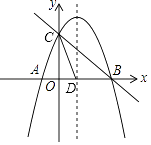
(1)求抛物线的解析式
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,请直接写出P点的坐标;如果不存在,请说明理由.
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?请求出△CBF的最大面积及此时E点的坐标.
相关试题

