【题目】我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1,1,系数和为2;(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1,系数和为4;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1,系数和为8……

根据以上规律,解答下列问题:
(1)(a+b)4的展开式共有多少项,系数分别为多少;
(2)写出(a+b)5的展开式;
(3)(a+b)n的展开式共有多少项,系数和为多少.
参考答案:
【答案】(1)5; 1,4,6,4,1;(2)a5+5a4b+10a3b2+10a2b3+5ab4+b5;(3)(n+1); 2n.
【解析】
(1)本题通过阅读理解寻找规律,观察可得(a+b)n(n为非负整数)展开式的各项系数的规律:首尾两项系数都是1,中间各项系数等于(a+b)n-1相邻两项的系数和.因此可得(a+b)4的各项系数分别为1、(1+3)、(3+3)、(3+1)、1即可;
(2)由(1)得出的规律,即可得出结果;
(3)根据题意得出(a+b)n展开式共有(n+1)项,当a=b=1时,(a+b)n=2n即可.
解:(1)根据题意知,(a+b)4的展开后,共有5项,
各项系数分别为1、(1+3)、(3+3)、(3+1)、1,
即:1、4、6、4、1;
(2)根据题意得:(a+b)5的展开式为a5+5a4b+10a3b2+10a2b3+5ab4+b5.
(3)根据题意得:(a+b)n的展开式共有(n+1)项
当a=b=1时,(a+b)n=2n.
即:(a+b)n的展开式系数和为2n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书? -
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数a,我们规定:用符号[
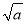 ]表示不大于
]表示不大于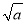 的最大整数,称[
的最大整数,称[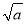 ]为a的根整数,例如:[
]为a的根整数,例如:[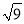 ]=3,[
]=3,[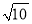 ]=3.
]=3.(1)仿照以上方法计算:[
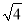 ] = ;[
] = ;[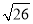 ] = .
] = .(2)若[
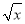 ]=1,写出满足题意的x的整数值 .
]=1,写出满足题意的x的整数值 .如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次 [
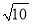 ]=3→[
]=3→[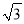 ]=1,这时候结果为1.
]=1,这时候结果为1.(3)对100连续求根整数, 次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
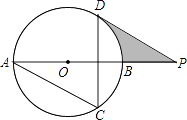
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】“五四”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号
进价(元/只)
售价(元/只)
A型
10
12
B型
15
23
(1)设购进A型文具x只,销售利润为w元,求w与x的函数关系式?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市购进一批文具袋,每个进价为10元.试销售期间,记录的每天的销售数量与销售单价的数据如下表:
销售单价x(元
11
12
13
14
15
…
销售数量y(个)
38
36
34
32
30
…
备注:物价局规定,每个文具袋的售价不低于10元且不高于18元
请你根据表中信息解答下列问题:
(1)y是x的函数,其函数关系式为
(2)营业员发现有一天的利润是150元,则销售单价为元.
(3)试销售的目的是想要每天获得最大的销售利润.请你帮助销售经理计算一下,在这种情况下单价x(元)应定为多少时,每天的销售利润w(元)最大,最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】将一张如图①所示的长方形铁皮四个角都剪去边长为30cm的正方形,再四周折起,做成一个有底无盖的铁盒,如图②.铁盒底面长方形的长是4acm,宽是3acm.

(1)请用含有a的代数式表示图①中原长方形铁皮的面积;
(2)若要在铁盒的外表面涂上某种油漆,每1元钱可涂油漆的面积为
 cm2,则在这个铁盒的外表面涂上油漆需要多少钱(用含有a的代数式表示)?
cm2,则在这个铁盒的外表面涂上油漆需要多少钱(用含有a的代数式表示)?
相关试题

