【题目】如图1,在△ABC中,AB=AC=2,∠A=90°,将一块与△ABC全等的三角板的直角顶点放在点C上,一直角边与BC重叠.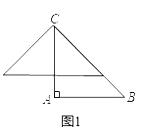
(1)操作1:固定△ABC,将三角板沿C→B方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿C→B方向平移的距离为;
(2)操作2:在(1)的情况下,将三角板BC的中点M顺时针方向旋转角度a(0°<a<90°),如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;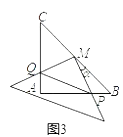
(3)在(2)的情形下,连PQ,则当△MPQ的面积等于四边形MPAQ的面积的一半时,四边形MPAQ的形状为 , 此时BP= .
参考答案:
【答案】
(1)![]()
(2)
答:四边形MPAQ的面积S不变.
解法1:连接AM,
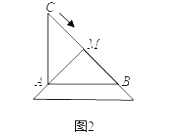

∵AB=AC=2,∠A=90°,
∴S△ABC= ![]() ABAC=
ABAC= ![]() ×2×2=2
×2×2=2
又由(1)知,点M是BC中点
∴∠CAM=∠BAM=∠B=45°,AM⊥BC,
∴AM=BM,∠BMP+∠PMA=90°
∴S△ABM= ![]() S△ABC=1
S△ABC=1
又∠AMQ+∠PMA=90°
∴∠AMQ=∠BMP
∴△AMQ≌△BMP
∴S四边形MPAQ=S△ABM=1,
解法2:如图3,作MD⊥AC于D,作ME⊥AB于E,
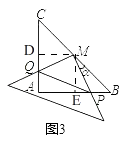
∵AB=AC=2,∠A=90°
∴∠B=∠C=45°,四边形ADME是矩形,
S△ABC= ![]() ABAC=
ABAC= ![]() ×2×2=2
×2×2=2
又∵点M是BC中点
∴Rt△CMD≌Rt△BME
∴四边形ADME是正方形,易求S正方形ADME= ![]() S△ABC=1
S△ABC=1
∴MD=ME,∠DMQ+∠QME=90°,
又∠EMP+∠QME=90°
∴∠DMQ=∠EMP
∴△DMQ≌△EMP
∴S四边形MPAQ=S正方形ADME=1,
(3)正方形;1
【解析】(1.)解:(1)BC= ![]() =2
=2 ![]() ,
,
∴CM= ![]() BC=
BC= ![]() 故三角板沿C→B方向平移的距离为:
故三角板沿C→B方向平移的距离为: ![]() ;
;
所以答案是: ![]() ;
;
(3.)设AQ=PB=x,AP=2﹣x,
S△MPQ=S四边形MAPQ﹣S△APQ=1﹣ ![]() AQAP=1﹣
AQAP=1﹣ ![]() x(2﹣x)=
x(2﹣x)= ![]() x2﹣x+1=
x2﹣x+1= ![]()
解得,x=1.
∴PB=1,
∴AQ=PB=AP=1,
∴点P是AB的中点,
∵M是BC中点,
∴PM∥AQ,
∴∠MPA=90°,
∵∠PAQ=∠PMQ=90°,
∴四边形MPAQ是矩形,
∵AQ=AP,
∴矩形MPAQ是正方形,
所以答案是:正方形,1.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对相似三角形的性质的理解,了解对应角相等,对应边成比例的两个三角形叫做相似三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五四”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号
进价(元/只)
售价(元/只)
A型
10
12
B型
15
23
(1)设购进A型文具x只,销售利润为w元,求w与x的函数关系式?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市购进一批文具袋,每个进价为10元.试销售期间,记录的每天的销售数量与销售单价的数据如下表:
销售单价x(元
11
12
13
14
15
…
销售数量y(个)
38
36
34
32
30
…
备注:物价局规定,每个文具袋的售价不低于10元且不高于18元
请你根据表中信息解答下列问题:
(1)y是x的函数,其函数关系式为
(2)营业员发现有一天的利润是150元,则销售单价为元.
(3)试销售的目的是想要每天获得最大的销售利润.请你帮助销售经理计算一下,在这种情况下单价x(元)应定为多少时,每天的销售利润w(元)最大,最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】将一张如图①所示的长方形铁皮四个角都剪去边长为30cm的正方形,再四周折起,做成一个有底无盖的铁盒,如图②.铁盒底面长方形的长是4acm,宽是3acm.

(1)请用含有a的代数式表示图①中原长方形铁皮的面积;
(2)若要在铁盒的外表面涂上某种油漆,每1元钱可涂油漆的面积为
 cm2,则在这个铁盒的外表面涂上油漆需要多少钱(用含有a的代数式表示)?
cm2,则在这个铁盒的外表面涂上油漆需要多少钱(用含有a的代数式表示)? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).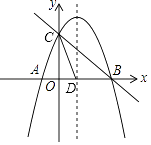
(1)求抛物线的解析式
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,请直接写出P点的坐标;如果不存在,请说明理由.
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?请求出△CBF的最大面积及此时E点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别
成绩x分
频数(人数)
第1组
25≤x<30
4
第2组
30≤x<35
6
第3组
35≤x<40
14
第4组
40≤x<45
a
第5组
45≤x<50
10
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?

-
科目: 来源: 题型:
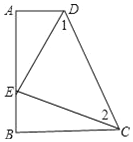
查看答案和解析>>【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
求证:(1)△ADE≌△BEC
(2)△CDE是直角三角形.
相关试题

