【题目】已知一块三角形的土地要分给甲、乙、丙三家农户. 如图,如果∠A=90°,∠B=30°.


(1)这三家农户所得土地的大小、形状都相同,请你在图中试着分一分,并简洁说明你的理由.
(2)要使这三家农户所得土地是面积相等的三角形,且有一个公共顶点,请你在备用图中试着分一分,并简洁说明你的理由.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)根据全等三角形的证明可以解决题目,因为要求大小形状都一样,所以要划分成3个全等的三角形.故可作作![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() .构造三个含30°全等的直角三角形即可.
.构造三个含30°全等的直角三角形即可.
(2)根据等底等高的三角形面积相等可知,将三角形一条边分三等分即可解答.
(1)解:作![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() .
.
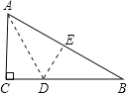
证明如下:![]() 是
是![]() 的垂直平分线
的垂直平分线
![]() ,
,![]() ,
,
在![]() 和
和![]() 中
中
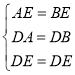 ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
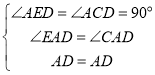 ,
,
![]()
![]() ,
,
![]() ,
,
∴把CD,DE作为这块三角形土地的分割线,分成的三块土地符合题设要求.
(2)解:如图所示,取线段BC的三等分点F ,G ,连结AF,AG.
则△ACF、△AFG、△AGB为所求.
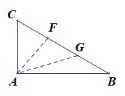
∵CF=FG=BG,
∴S△ACF=S△AFG=S△AGB=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要在湖两岸A,B两点之间修建一座观赏桥,由于条件限制,无法直接测量A、B两点间的距离,于是小明想出来这样一种做法:在AB的垂线BF上取两点C、D,使BC=CD,再定出BF的垂线DE,使A,C,E三点在一条直线上,这时测得DE=50米,则AB=_________米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.
(1)求证:AE=FB;
(2)在不添加任何辅助线的情况下,请直接写出所有与△ABM全等的三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,轮船从A港出发,以28海里/小时的速度向正北方向航行,此时测的灯塔M在北偏东30°的方向上.半小时后,轮船到达B处,此时测得灯塔M在北偏东60°的方向上.
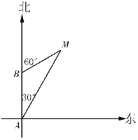
(1)求轮船在B处时与灯塔M的距离;
(2)轮船从B处继续沿正北方向航行,又经半小时后到达C处.求:此时轮船与灯塔M的距离是多少?灯塔M在轮船的什么方向上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,计算下列五角星图案中五个顶角的度数和. 即:求∠A+∠B+∠C+∠D+∠E的大小.
(2)如图2,若五角星的五个顶角的度数相等, 求∠1的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,点D在AC上,点E在BA的延长线上,BD与CE相交于点F, 且BD=CE.

(1)求证:BF⊥CE.
(2)如图2,连结AF ,证明AF平分∠BFE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )


A. 两人从起跑线同时出发,同时到达终点
B. 小苏跑全程的平均速度大于小林跑全程的平均速度
C. 小苏前15s跑过的路程大于小林前15s跑过的路程
D. 小林在跑最后100m的过程中,与小苏相遇2次
相关试题

