【题目】如图1,在矩形ABCD中,点A(1,1),B(3,1),C(3,2),反比例函数y=![]() (x>0)的图象经过点D,且与AB相交于点E,
(x>0)的图象经过点D,且与AB相交于点E,
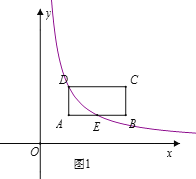
(1)求反比例函数的解析式;
(2)过点C、E作直线,求直线CE的解析式;
(3)如图2,将矩形ABCD沿直线CE平移,使得点C与点E重合,求线段BD扫过的面积.

参考答案:
【答案】(1)反比例函数的解析式为y=![]() ; (2)直线CE的解析式为y=x-1;(3) 3.
; (2)直线CE的解析式为y=x-1;(3) 3.
【解析】分析:(1)由矩形的性质求得点D的坐标,即可求得k;(2)根据反比例函数的解析式求点E的坐标,用待定系数法求直线CE的解析式;(3)BD扫过的面积是一个平行四边形,它的面积=2S△BB′D′.
详解:(1)由题意得AD=CB=1,故点D的坐标为(1,2),
∵函数y=![]() 的图象经过点D(1,2),
的图象经过点D(1,2),
∴2=![]() .∴m=2,
.∴m=2,
∴反比例函数的解析式为y=![]() ;
;
(2)当y=1时,1=![]() .∴x=2,∴E(2,1),
.∴x=2,∴E(2,1),
设直线CE的解析式为y=kx+b,根据题意得![]()
解得![]()
∴直线CE的解析式为y=x-1;
(3)∵矩形ABCD沿直线CE平移,使得点C与点E重合,点D(0,1),B'(2,0),
S四边形BDD′B′=2S△BB′D′=2×![]() ×3×1=3.
×3×1=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市电力部门对一般照明用电实行“阶梯电价”收费,具体收费标准如下:
第一档:月用电量不超过240度的部分的电价为每度0.6元;
第二档:月用电量超过240度但不超过400度部分的电价为每度0.65元;
第三档:月用电量超过400度的部分的电价为每度0.9元.
(1)已知老王家去年5月份的用电量为380度,则老王家5月份应交电费 元;
(2)若去年6月份老王家用电的平均电价为0.70元,求老王家去年6月份的用电量;
(3)已知老王家去年7、8月份的用电量共500度(7月份的用电量少于8月份的用电量),两个月的总电价是303元,求老王家7、8月的用电量分别是多少?
-
科目: 来源: 题型:
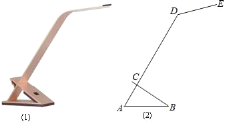
查看答案和解析>>【题目】如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.
(1)求DE与水平桌面(AB所在直线)所成的角;
(2)求台灯的高(点E到桌面的距离,结果精确到0.1cm).
(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,sin30°=0.5,cos30°=0.87,tan30°=0.58.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC是直线AE外两点,且∠1=∠2,要得到△ABE≌△ACE,需要添加的条件有①AB=AC;②BE=CE;③∠B=∠C;④∠AEB=∠AEC;⑤∠BAE=∠CAE.其中正确的( )

A.①②③B.②③④C.②③⑤D.①④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180°时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△ABC与△DAE互为“顶补三角形”,AM,AN是“顶心距”.
①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM= DE;
②如图3,当∠BAC=120°,BC=6时,AN的长为 .
猜想论证:
(2)在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,AD=AB,CD=BC,∠B=90°,∠A=60°,CD=2,在四边形ABCD的内部是否存在点P,使得△PAD与△PBC互为“顶补等腰三角形”?若存在,请给予证明,并求△PBC的“顶心距”的长;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=BC,AB⊥BC,过点B作直线l,过点A作AE⊥l于E,过点C作CF⊥l于F,则下列说法中正确的是( )

A.AC=AE+BEB.EF=AE+EBC.AC=EB+CFD.EF=EB+CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中:
①已知两实数a、b,如果a>b,那么a2>b2;②同位角相等,两直线平行;③如果两个角是直角,那么这两个角相等;④如果分式
 无意义,那么x=﹣
无意义,那么x=﹣ ;这些命题及其逆命题都是真命题的是( )
;这些命题及其逆命题都是真命题的是( )A.①②B.③④C.①③D.②④
相关试题

