【题目】超速行驶是引发交通事故的主要原因.上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,观测点设在到公路l的距离为100米的P处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度?

参考答案:
【答案】此车超过每小时80千米的限制速度.
【解析】试题分析: 首先,根据在直角三角形BPO中,∠BPO=45°,可得到BO=PO=100m,再根据在直角三角形APO中,∠APO=60°,运用三角函数值,可得到AO=100![]() ,根据AB=AO-BO可求得AB的长;再结合速度的计算方法,求出车的速度,然后将车的速度与80千米/时进行比较,即可得到结论.
,根据AB=AO-BO可求得AB的长;再结合速度的计算方法,求出车的速度,然后将车的速度与80千米/时进行比较,即可得到结论.
试题解析:
解:在Rt△APO中,∠APO=60°,则∠PAO=30°.
∴AP=2OP=200 m,
AO=![]() =
=![]() =100
=100![]() (m).
(m).
在Rt△BOP中,∠BPO=45°,
则BO=OP=100 m.
∴AB=AO-BO=100![]() -100≈73(m).
-100≈73(m).
∴从A到B小车行驶的速度为73÷3≈24.3(m/s)=87.48 km/h>80 km/h.
∴此车超过每小时80千米的限制速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线与x轴交于点A(﹣5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.

(1)求抛物线的解析式;
(2)当点M和N都在线段AC上时,连接MF,如果sin∠AMF= ,求点Q的坐标;
,求点Q的坐标;
(3)在矩形的平移过程中,当以点P,Q,M,N为顶点的四边形是平行四边形时,求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEC中,AB=DE.若添加条件后使得△ABC≌△DEC,则在下列条件中,不能添加的是( )

A. BC=EC,∠B=∠E B. BC=EC,AC=DC
C. ∠B=∠E,∠A=∠D D. BC=EC,∠A=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
①3-2
 =(
=( -1)2;
-1)2;②5-2
 =(
=( -
- )2;
)2;③7-2
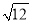 =(
=( -
- )2;…
)2;…(1)请你根据以上规律,写出第6个等式 .
(2)第n个等式可以表示为 ,并请你证明你得到的等式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+2
x+2  与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和
与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和  个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
(1)求点A,点B的坐标;
(2)用含t的代数式分别表示EF和AF的长;
(3)当四边形ADEF为菱形时,试判断△AFG与△AGB是否相似,并说明理由.
(4)是否存在t的值,使△AGF为直角三角形?若存在,求出这时抛物线的解析式;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.

(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.
相关试题

