【题目】在如图所示的方格纸中,点P是∠AOC的边OA上一点,仅用无刻度的直尺完成如下操作:
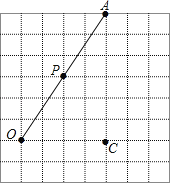
(1)过点P画OC的垂线,垂足为点H;
(2)过点P画OA的垂线,交射线OC于点B;
(3)分别比较线段PB与OB的大小:PB OB(填“>”“<”或“=”),理由是 .
参考答案:
【答案】(1)如图所示:点H即为所求;见解析;(2)如图所示:点B即为所求;见解析;(3)<,直线外一点与直线上各点连接的所有线段中,垂线段最短.
【解析】
(1)直接利用垂线的作法得出答案;
(2)结合网格得出过点![]() 的
的![]() 垂线
垂线![]() 即可;
即可;
(3)利用垂线的性质得出答案.
(1)如图所示:点H即为所求;
(2)如图所示:点B即为所求;
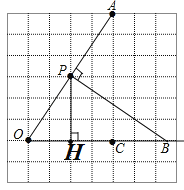
(3)PB<OB,
理由是:直线外一点与直线上各点连接的所有线段中,垂线段最短.
故答案为:<,直线外一点与直线上各点连接的所有线段中,垂线段最短.
-
科目: 来源: 题型:
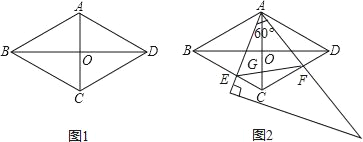
查看答案和解析>>【题目】如图1,在菱形ABCD中,AC=2,BD=2
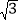 ,AC、BD相交于点O.
,AC、BD相交于点O.(1)AB的长为 ;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①求证:△ABE≌△ACF;
②判断△AEF是哪一种特殊三角形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
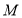 是定长线段
是定长线段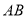 上一定点,点
上一定点,点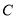 在线段
在线段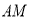 上,点
上,点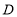 在线段
在线段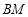 上,点
上,点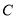 、点
、点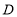 分别从点
分别从点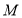 、点
、点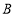 出发以
出发以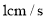 、
、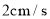 的速度沿直线
的速度沿直线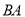 向左运动,运动方向如箭头所示.
向左运动,运动方向如箭头所示.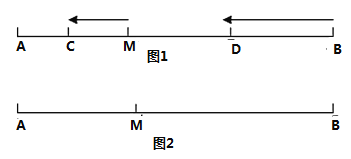
(1)若
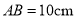 ,当点C、D运动了2s,求
,当点C、D运动了2s,求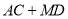 的值;
的值;(2)若点
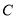 、
、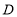 运动时,总有
运动时,总有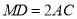 ,直接填空:
,直接填空: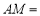 ______
______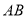 ;
;(3)在(2)的条件下,
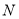 是直线
是直线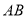 上一点,且
上一点,且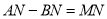 ,求
,求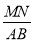 的值.
的值. -
科目: 来源: 题型:
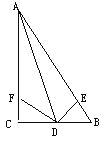
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=
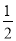 ∠BAD.求证:EF=BE+FD;
∠BAD.求证:EF=BE+FD;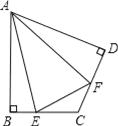
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=
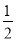 ∠BAD,(1)中的结论是否仍然成立?
∠BAD,(1)中的结论是否仍然成立?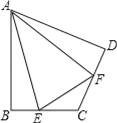
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=
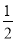 ∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.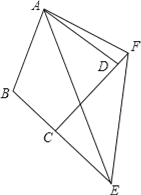
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(5,3),点B(-3,3),过点A的直线
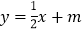 (m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D。
(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D。(1)求点P的坐标;
(2)求直线BP的解析式,并直接写出△PCD与△PAB的面积比;
(3)若反比例函数
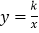 (k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值。
(k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值。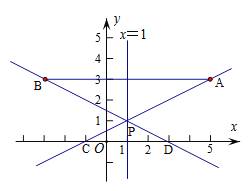
相关试题

