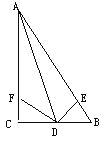
【题目】如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长。
参考答案:
【答案】(1)见解析;(2)2
【解析】试题分析:(1)根据角平分线的性质“角平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离即DE=CD,再根据HL证明Rt△CDF≌Rt△EBD,从而得出CF=EB;
(2)设CF=x,则AE=12-x,再根据题意得出△ACD≌△AED,进而可得出结论.
试题解析:
(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在△CDF与△EDB中,
![]()
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)解:设CF=x,则AE=12-x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在△ACD与△AED中,
![]()
∴△ACD≌△AED(HL),
∴AC=AE,即8+x=12-x,
解得x=2,即CF=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2﹣12x+18= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线的解析式为
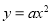 ,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点
,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点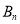 (
( ,0 ) (n为正整数 )作x轴的垂线,交抛物线于点
,0 ) (n为正整数 )作x轴的垂线,交抛物线于点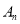 ,连接
,连接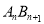 ,得直角三角形
,得直角三角形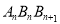 .
.(1)求a的值;
(2)直接写出线段
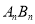 ,
,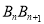 的长(用含n的式子表示);
的长(用含n的式子表示);(3)在系列Rt△
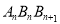 中,探究下列问题:
中,探究下列问题:①当n为何值时,Rt△
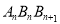 是等腰直角三角形?
是等腰直角三角形?②设1≤k<m≤n (k,m均为正整数),问是否存在Rt△
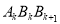 与Rt△
与Rt△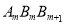 相似?若存在,求出其相似比;若不存在,说明理由.
相似?若存在,求出其相似比;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:

(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,上海市全社会用于环境保护的资金约为90 800 000 000元,这个数用科学记数法表示为( ).
A.908×108B.90.8×109C.9.08×1011D.9.08×1010.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果将抛物线y=x2向上平移1个单位,那么所得抛物线对应的函数关系式是( )
A.y=x2+1B.y=x2﹣1C.y=(x+1)2D.y=(x﹣1)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰三角形ABC中,AB=AC,一腰上的中线等腰三角形ABC的周长分成15和6两部分,求三角形ABC的腰长及底边长。
相关试题

