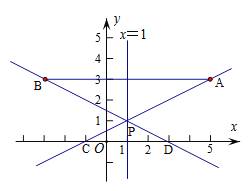
【题目】如图,在平面直角坐标系中,已知点A(5,3),点B(-3,3),过点A的直线![]() (m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D。
(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D。
(1)求点P的坐标;
(2)求直线BP的解析式,并直接写出△PCD与△PAB的面积比;
(3)若反比例函数![]() (k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值。
(k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值。
参考答案:
【答案】(1)P(1,1); (2)![]() ;(3)当k<0时,最小值为-9;当k>0时,最大值为
;(3)当k<0时,最小值为-9;当k>0时,最大值为![]()
【解析】试题分析:![]() 把点
把点![]() 坐标代入一次函数
坐标代入一次函数![]() ,求得
,求得![]() 的值,进而求得点
的值,进而求得点![]() 的坐标.
的坐标.
![]() 用待定系数法即可求得直线
用待定系数法即可求得直线![]() 的解析式,直接计算面积即可求出它们的比值.
的解析式,直接计算面积即可求出它们的比值.
![]() 分成
分成![]() 和
和![]() 两种情况进行讨论.
两种情况进行讨论.
试题解析:(1)∵![]() 过点A(5,3),
过点A(5,3),
![]()
解得:![]()
∴y=![]() ,
,
当![]() 时,∴
时,∴![]() ,
,
∴![]()
(2)设直线BP的解析式为y=ax+b,
根据题意,得![]()
解得: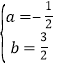
∴直线BP的解析式为![]() ,
,
点![]()
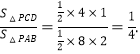
(3)当![]() 时,经过点
时,经过点![]() 时,有最值为-9;
时,有最值为-9;
当![]() 时,联立方程
时,联立方程 整理得,
整理得,![]()
![]() 解得:
解得:![]()
即最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格纸中,点P是∠AOC的边OA上一点,仅用无刻度的直尺完成如下操作:
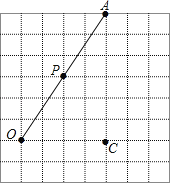
(1)过点P画OC的垂线,垂足为点H;
(2)过点P画OA的垂线,交射线OC于点B;
(3)分别比较线段PB与OB的大小:PB OB(填“>”“<”或“=”),理由是 .
-
科目: 来源: 题型:
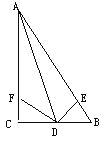
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=
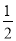 ∠BAD.求证:EF=BE+FD;
∠BAD.求证:EF=BE+FD;
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=
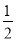 ∠BAD,(1)中的结论是否仍然成立?
∠BAD,(1)中的结论是否仍然成立?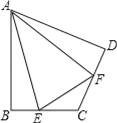
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=
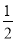 ∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.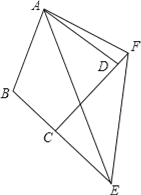
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B在长方形的边上.
(1)用圆规和无刻度的直尺在长方形的内部作∠ABC=∠ABO;(保留作图痕迹,不写作法)
(2)在(1)的条件下,若BE是∠CBD的角平分线,探索AB与BE的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O在线段AB上,(不与端点A、B重合),以点O为圆心,OA的长为半径画弧,线段BP与这条弧相切与点P,直线CD垂直平分PB,交PB于点C,交AB于点D,在射线DC上截取DE,使DE=DB。已知AB=6,设OA=r。
(1)求证:OP∥ED;
(2)当∠ABP=30°时,求扇形AOP的面积,并证明四边形PDBE是菱形;
(3)过点O作OF⊥DE于点F,如图所示,线段EF的长度是否随r的变化而变化?若不变,直接写出EF的值;若变化,直接写出EF与r的关系。


-
科目: 来源: 题型:
查看答案和解析>>【题目】给出定义:我们用(a,b)来表示一对有理数a,b,若a,b满足a﹣b=ab+1,就称(a,b)是“泰兴数”如2﹣
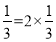 +1,则(2,
+1,则(2,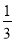 )是“泰兴数”.
)是“泰兴数”.(1)数对(﹣2,1),(5,
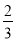 )中是“泰兴数”的是 .
)中是“泰兴数”的是 .(2)若(m,n)是“泰兴数”,求6m﹣2(2m+mn)﹣2n的值;
(3)若(a,b)是“泰兴数”,则(﹣a,﹣b) “泰兴数”(填“是”或“不是”).
相关试题

