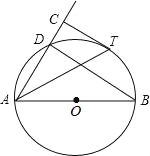
【题目】如图,AB是⊙O的直径,D为⊙O上一点,过![]() 上一点T作⊙O的切线TC,且TC⊥AD于点C.
上一点T作⊙O的切线TC,且TC⊥AD于点C.
(1)若∠DAB=50°,求∠ATC的度数;
(2)若⊙O半径为2,CT=![]() ,求AD的长.
,求AD的长.
参考答案:
【答案】(1)、65°;(2)、2.
【解析】
试题分析:(1)、连接OT,根据同角的余角相等得出∠CAD=∠ATO,进而得出∠DAB=2CAT,解答即可;(2)、过O作OE⊥AC于E,连接OT、OD,得出矩形OECT,求出OT=CE,根据垂径定理求出DE,根据矩形性质求出OT=CT,根据勾股定理求出即可.
试题解析:(1)、连接OT,如图1:
∵TC⊥AD,⊙O的切线TC, ∴∠ACT=∠OTC=90°, ∴∠CAT+∠CTA=∠CTA+∠ATO, ∴∠CAT=∠ATO,
∵OA=OT, ∴∠OAT=∠ATO, ∴∠DAB=2∠CAT=50°, ∴∠CAT=25°, ∴∠ATC=90°﹣25°=65°;
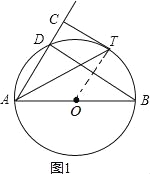
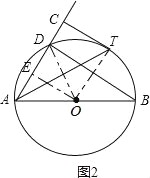
(2)、过O作OE⊥AC于E,连接OT、OD,如图2:
∵AC⊥CT,CT切⊙O于T, ∴∠OEC=∠ECT=∠OTC=90°, ∴四边形OECT是矩形,
∴OT=CE=OD=2, ∵OE⊥AC,OE过圆心O, ∴AE=DE=![]() AD, ∵CT=OE=
AD, ∵CT=OE=![]() ,
,
在Rt△OED中,由勾股定理得:ED=1, ∴AD=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(a,b)在第三象限,则M(-ab,-a)应在 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )
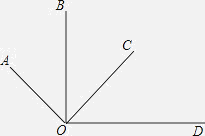
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.①②③
B.①②④
C.①③④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A1,A2,…,An均在直线y=x﹣1上,点B1,B2,…,Bn均在双曲线y=﹣
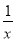 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=﹣1,则a2016= .
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=﹣1,则a2016= .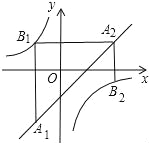
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠BAC=90°,AD⊥BC于D,则下列结论中,正确的个数为( ). ①AB⊥AC; ②AD与AC互相垂直; ③点C到AB的垂线段是线段AB; ④点D到BC的距离是线段AD的长度; ⑤线段AB的长度是点B到AC的距离; ⑥线段AB是点B到AC的距离; ⑦AD>BD.

A.2个
B.4个
C.7个
D.0个 -
科目: 来源: 题型:
查看答案和解析>>【题目】3xm+5y2与xyn是同类项,则mn的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB、AC引垂线,垂足分别为E、F点.
(1)当点D在BC的什么位置时,DE=DF?并证明.
(2)在满足第一问的条件下,连接AD,此时图中共有几对全等三角形?并请给予写出(不 必证明).
(3)过C点作AB边上的高CG,请问DE、DF、CG的长之间存在怎样的等量关系?并加以证明.

相关试题

