【题目】如图1,在△ABC中,AB=BC=5,AC=6,△ABC沿BC方向向右平移得△DCE,A、C对应点分别是D、E.AC与BD相交于点O.
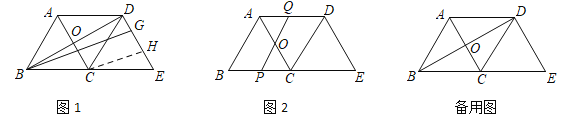
(1)将射线BD绕B点顺时针旋转,且与DC,DE分别相交于F,G,CH∥BG交DE于H,当DF=CF时,求DG的长;
(2)如图2,将直线BD绕点O逆时针旋转,与线段AD,BC分别相交于点Q,P.设OQ=x,四边形ABPQ的周长为y,求y与x之间的函数关系式,并求y的最小值.
(3)在(2)中PQ的旋转过程中,△AOQ是否构成等腰三角形?若能构成等腰三角形,求出此时PQ的长?若不能,请说明理由.
参考答案:
【答案】(1)2;(2)y=2x+10(![]() ≤x≤4),当x=
≤x≤4),当x=![]() 时,y有最小值,最小值为
时,y有最小值,最小值为![]() ;(3)能,满足条件的PQ的值为:
;(3)能,满足条件的PQ的值为:![]() 或5或6.
或5或6.
【解析】
(1)证明DG=GH=EH即可解决问题.
(2)如图2中,作AH⊥BC于H.解直角三角形求出AH,可得OQ的最小值,证明△AOQ≌△COP(ASA),推出AQ=PC,推出y=AQ+AB+BP+PC+PQ=AB+BC+PQ=10+2x(![]() ≤x≤4).根据一次函数的性质求出最值即可.
≤x≤4).根据一次函数的性质求出最值即可.
(3)分三种情形:①当AQ=AO=3时,作OH⊥AD于H.②当点Q是AD的中点时.③当OA=OQ=3时,分别求解即可.
解:(1)如图中,
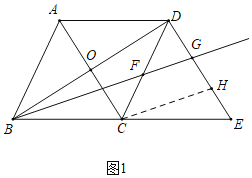
∵DF=FC,CH∥FG,
∴DG=GH,
∵BC=CE,CH∥BG,
∴GH=HE,
∴DG=GH=HE,
∴DG=![]() DE=
DE=![]() AC=2.
AC=2.
(2)如图2中,作AH⊥BC于H.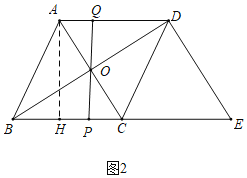
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,
∴OA=OC=3,OB=OD=![]() =4,
=4,
∴![]() ,
,
∴AH=![]() ,
,
∵AQ∥PC,
∴∠QAO=∠PCO,
∵OA=OC,∠AOQ=∠COP,
∴△AOQ≌△COP(ASA),
∴AQ=PC,
∴y=AQ+AB+BP+PC+PQ=AB+BC+PQ=10+2x(![]() ≤x≤4).
≤x≤4).
∴y=2x+10(![]() ≤x≤4).
≤x≤4).
当x=![]() 时,y有最小值,最小值为
时,y有最小值,最小值为![]() .
.
(3)能;
如图3中,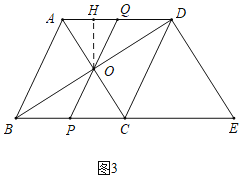
分三种情形:①当AQ=AO=3时,作OH⊥AD于H.
易知OH=![]() ,
,
∴AH=![]() =
=![]() ,
,
∴HQ=![]() ,
,
∴OQ=![]() ,
,
∴PQ=2OQ=![]() .
.
②当点Q是AD的中点时,AQ=OQ=DQ=![]() ,
,
∴PQ=2OQ=5.
③当OA=OQ=3时,PQ=2OQ=6.
综上所述,满足条件的PQ的值为:![]() 或5或6.
或5或6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个形如六边形的点阵,它的中心是一个点,算做第一层,第二层每边两个点,第三层每边三个点,以此类推.

(1)填写下表:
层数
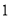

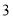

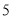
该层对应的点数
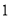
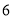
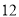
________
________
(2)写出第
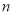 层对应的点数(
层对应的点数(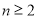 );
); -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,网格图由边长为1的小正方形所构成,Rt△ABC的顶点分别是A(-1,3),B(-3,-1),C(-3,3).

(1)请在图1中作出△ABC关于点(-1,0)成中心对称△
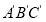 ,并分别写出A,C对应点的坐标
,并分别写出A,C对应点的坐标 ;
;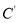
(2)设线段AB所在直线的函数表达式为
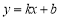 ,试写出不等式
,试写出不等式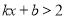 的解集是 ;
的解集是 ;(3)点M和点N 分别是直线AB和y轴上的动点,若以
 ,
,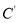 ,M,N为顶点的四边形是平行四边形,求满足条件的M点坐标.
,M,N为顶点的四边形是平行四边形,求满足条件的M点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是
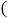

A. 四边形的内角和小于外角和 B.
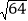 的立方根为4
的立方根为4C. 一元二次方程
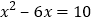 无实数根 D. 分式方程
无实数根 D. 分式方程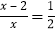 的解为4
的解为4 -
科目: 来源: 题型:
查看答案和解析>>【题目】为保持水土,美化环境,W中学准备在从校门口到柏油公路的这一段土路的两侧栽一些树,并要求土路两侧树的棵数相等间距也相等,且首、尾两端均栽上树,现在学校已备好一批树苗,若间隔30米栽一棵,则缺少22棵;若间隔35米栽一棵,则缺少14棵
(1)求学校备好的树苗棵数.
(2)某苗圃负责人听说W中学想在校外土路两旁栽树的上述情况后,觉得两树间距太大,既不美观,又影响防风固沙的效果,决定无偿支援W中学300棵树苗.请问,这些树苗加上学校自己备好的树苗,间隔5米栽一棵,是否够用?
-
科目: 来源: 题型:
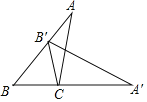
查看答案和解析>>【题目】如图,将
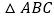 绕点C顺时针旋转,使点B落在AB边上点
绕点C顺时针旋转,使点B落在AB边上点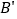 处,此时点A的对应点
处,此时点A的对应点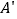 恰好落在BC的延长线上,下列结论错误的是
恰好落在BC的延长线上,下列结论错误的是
A.
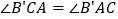 B.
B. 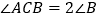
C.
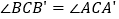 D.
D. 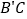 平分
平分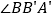
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
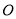 为直线
为直线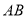 上一点,过点
上一点,过点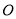 作射线
作射线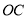 ,
,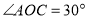 ,将一直角三角板(
,将一直角三角板(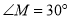 )的直角顶点放在点
)的直角顶点放在点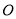 处,一边
处,一边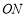 在射线
在射线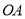 上,另一边
上,另一边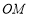 与
与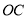 都在直线
都在直线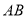 的上方.
的上方.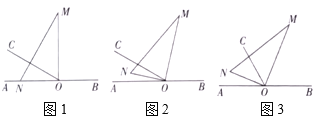
(1)将图1中的三角板绕点
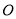 以每秒
以每秒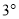 的速度沿顺时针方向旋转一周.如图2,经过
的速度沿顺时针方向旋转一周.如图2,经过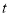 秒后,边
秒后,边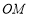 恰好平分
恰好平分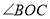 .求
.求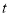 的值;
的值;(2)在(1)问条件的基础上,若三角板在转动的同时,射线
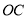 也绕
也绕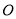 点以每秒
点以每秒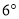 的速度沿顺时针方向旋转一周,如图3,那么经过多长时间
的速度沿顺时针方向旋转一周,如图3,那么经过多长时间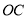 平分
平分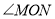 ?请说明理由;
?请说明理由;
相关试题

