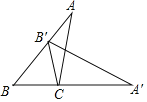
【题目】如图,将![]() 绕点C顺时针旋转,使点B落在AB边上点
绕点C顺时针旋转,使点B落在AB边上点![]() 处,此时点A的对应点
处,此时点A的对应点![]() 恰好落在BC的延长线上,下列结论错误的是
恰好落在BC的延长线上,下列结论错误的是![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]() 平分
平分![]()
参考答案:
【答案】A
【解析】分析:利用旋转的性质可对C直接进行判断;利用CB=CB′得到∠B=∠CB′B,再利用三角形外角性质得到∠A′CB′=∠B+∠CB′B,所以∠ACB=2∠B,则可对B进行判断;利用∠B=∠CB′B,∠B=∠CB′A′可对D进行判断.
详解:∵△ABC绕点C顺时针旋转,使点B落在AB边上点B′处,此时点A的对应点A′恰好落在BC的延长线上,
∴CB=CB′,CA=CA′,∠BCB′=∠ACA′,∠A=∠A′,∠B=∠CB′A′,∠ACB=∠A′CB′,所以C选项正确;
∵∠A′CB′=∠B+∠CB′B,
而CB=CB′,
∴∠B=∠CB′B,
∴∠ACB=2∠B;所以B选项正确;
∵∠B=∠CB′B,∠B=∠CB′A′,
∴∠CB′B=∠CB′A′,
∴B′C平分∠BB′A′,所以D选项正确;
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是

A. 四边形的内角和小于外角和 B.
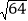 的立方根为4
的立方根为4C. 一元二次方程
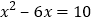 无实数根 D. 分式方程
无实数根 D. 分式方程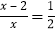 的解为4
的解为4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=BC=5,AC=6,△ABC沿BC方向向右平移得△DCE,A、C对应点分别是D、E.AC与BD相交于点O.
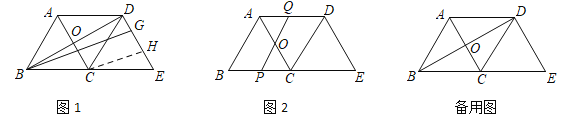
(1)将射线BD绕B点顺时针旋转,且与DC,DE分别相交于F,G,CH∥BG交DE于H,当DF=CF时,求DG的长;
(2)如图2,将直线BD绕点O逆时针旋转,与线段AD,BC分别相交于点Q,P.设OQ=x,四边形ABPQ的周长为y,求y与x之间的函数关系式,并求y的最小值.
(3)在(2)中PQ的旋转过程中,△AOQ是否构成等腰三角形?若能构成等腰三角形,求出此时PQ的长?若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保持水土,美化环境,W中学准备在从校门口到柏油公路的这一段土路的两侧栽一些树,并要求土路两侧树的棵数相等间距也相等,且首、尾两端均栽上树,现在学校已备好一批树苗,若间隔30米栽一棵,则缺少22棵;若间隔35米栽一棵,则缺少14棵
(1)求学校备好的树苗棵数.
(2)某苗圃负责人听说W中学想在校外土路两旁栽树的上述情况后,觉得两树间距太大,既不美观,又影响防风固沙的效果,决定无偿支援W中学300棵树苗.请问,这些树苗加上学校自己备好的树苗,间隔5米栽一棵,是否够用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
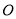 为直线
为直线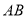 上一点,过点
上一点,过点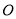 作射线
作射线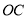 ,
,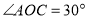 ,将一直角三角板(
,将一直角三角板(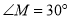 )的直角顶点放在点
)的直角顶点放在点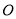 处,一边
处,一边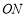 在射线
在射线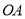 上,另一边
上,另一边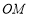 与
与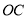 都在直线
都在直线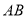 的上方.
的上方.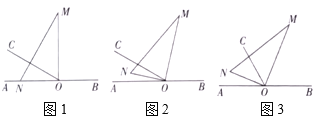
(1)将图1中的三角板绕点
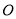 以每秒
以每秒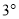 的速度沿顺时针方向旋转一周.如图2,经过
的速度沿顺时针方向旋转一周.如图2,经过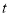 秒后,边
秒后,边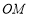 恰好平分
恰好平分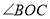 .求
.求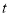 的值;
的值;(2)在(1)问条件的基础上,若三角板在转动的同时,射线
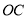 也绕
也绕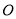 点以每秒
点以每秒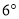 的速度沿顺时针方向旋转一周,如图3,那么经过多长时间
的速度沿顺时针方向旋转一周,如图3,那么经过多长时间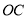 平分
平分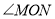 ?请说明理由;
?请说明理由; -
科目: 来源: 题型:
查看答案和解析>>【题目】去年7月份小明到银行开户,存入1500元,以后每月根据收支情况存入一笔钱,下表为该人从8月份到12月份的存款情况:则截止到去年12月份,存折上共有( )元钱.

A.9750B.8050C.1750D.9550
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将3个同样的正方体重叠放置在桌面上,每个正方体的6个面上分别写有-3、-2、-1、1、2、3,相对的两面上写的数字互为相反数,现在有5个面的数字无论从哪个角度都看不到,这5个看不到的面上数字的乘积是________.
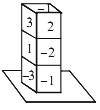
相关试题

