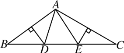
【题目】如图,在△ABC中,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,连接AD,AE.
(1)若∠BAC=110°,求∠DAE的度数;
(2)若∠BAC=θ(0°<θ<180°),求∠DAE的度数.(用含θ的式子表示)
参考答案:
【答案】(1) 40°;(2) ①∠DAE=2θ-180°,②∠DAE=180°-2θ.
【解析】
(1)根据线段的垂直平分线的性质得到DB=DA,EC=EA,根据等腰三角形的性质解答即可;
(2)分两种情况进行讨论,先根据线段垂直平分线的性质,得到∠B=∠BAD,∠C=∠CAE,进而得到∠BAD+∠CAE=∠B+∠C=180°-α,再根据角的和差关系进行计算即可.
(1)∵AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,
∴DB=DA,EC=EA.
∵∠BAC=110°,
∴∠B+∠C=70°.
∵DB=DA,EC=EA,
∴∠DAB=∠B,∠EAC=∠C,
∴∠DAB+∠EAC=70°,
∴∠DAE=110°-70°=40°.
(2)分两种情况:
①如答图1所示,当∠BAC≥90°时,
∵DM垂直平分AB,
∴DA=DB,
∴∠B=∠BAD.
同理可得,∠C=∠CAE,
∴∠BAD+∠CAE=∠B+∠C=180°-θ,
∴∠DAE=∠BAC-(∠BAD+∠CAE)=θ-(180°-θ)=2θ-180°.
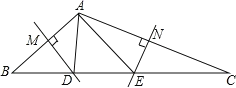
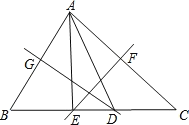
答图1 答图2
②如答图2所示,当∠BAC<90°时,
∵DM垂直平分AB,
∴DA=DB,
∴∠B=∠BAD.
同理可得,∠C=∠CAE,
∴∠BAD+∠CAE=∠B+∠C=180°-θ,
∴∠DAE=∠BAD+∠CAE-∠BAC=180°-θ-θ=180°-2θ.
-
科目: 来源: 题型:
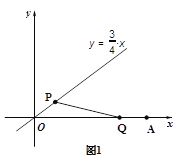
查看答案和解析>>【题目】已知在平面直角坐标系中,A(9,0),直线l:y=
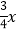 .P,Q两点分别同时从O,A出发,P点沿直线l向上运动,Q点沿x轴向左运动,它们的速度相同.连接PQ,当
.P,Q两点分别同时从O,A出发,P点沿直线l向上运动,Q点沿x轴向左运动,它们的速度相同.连接PQ,当PQ⊥x轴时,P,Q两点同时停止运动.设P点的横坐标为m(m≥0),
(1)求m的取值范围;
(2)如图1,当△OPQ是以OP为腰的等腰三角形时,求m的值;
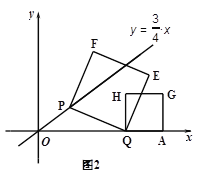
(3)如果以PQ为边在上方作正方形PQEF,以AQ为边在上方作正方形 QAGH,如图2,
①用含m的代数式表示E点的坐标;
②当正方形PQEF的某个顶点(Q点除外)落在正方形 QAGH的边上,请直接写出m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,然后解答问题:
分解因式:x3+3x2-4.
解答:把x=1代入多项式x3+3x2-4,发现此多项式的值为0,由此确定多项式x3+3x2-4中有因式(x-1),于是可设x3+3x2-4=(x-1)(x2+mx+n),分别求出m,n的值,再代入x3+3x2-4=(x-1)(x2+mx+n),就容易分解多项式x3+3x2-4.这种分解因式的方法叫“试根法”.
(1)求上述式子中m,n的值;
(2)请你用“试根法”分解因式:x3+x2-16x-16.
-
科目: 来源: 题型:
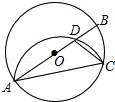
查看答案和解析>>【题目】如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数为度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000037毫克可用科学记数法表示为
A. 3.7×10﹣5克 B. 3.7×10﹣6克 C. 37×10﹣7克 D. 3.7×10﹣8克
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=
 x﹣3与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最大值是 .
x﹣3与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最大值是 . 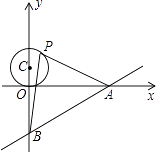
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?

相关试题

