【题目】已知在平面直角坐标系中,A(9,0),直线l:y=![]() .P,Q两点分别同时从O,A出发,P点沿直线l向上运动,Q点沿x轴向左运动,它们的速度相同.连接PQ,当
.P,Q两点分别同时从O,A出发,P点沿直线l向上运动,Q点沿x轴向左运动,它们的速度相同.连接PQ,当
PQ⊥x轴时,P,Q两点同时停止运动.设P点的横坐标为m(m≥0),
(1)求m的取值范围;
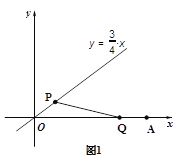
(2)如图1,当△OPQ是以OP为腰的等腰三角形时,求m的值;
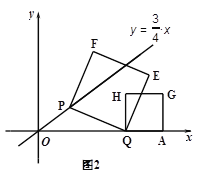
(3)如果以PQ为边在上方作正方形PQEF,以AQ为边在上方作正方形 QAGH,如图2,
①用含m的代数式表示E点的坐标;
②当正方形PQEF的某个顶点(Q点除外)落在正方形 QAGH的边上,请直接写出m的值.
参考答案:
【答案】(1)0≤m≤4;(2)![]() 或
或![]() .(3)①E(9-
.(3)①E(9-![]() m,9-
m,9-![]() );②m=4,
);②m=4, ![]() ,
,![]() .
.
【解析】
(1)直接将m点带入一次函数即可.
(2)讨论两个腰相等.
(3)过PE引x轴垂线,再讨论.
把x=m带入y= ![]() x得y=
x得y=![]() m,
m,
∴P(m,![]() m),∴OP=
m),∴OP=![]() =
=![]() ,
,
∵OP=AQ,∴AQ=![]() ,
,
∴OQ=9-![]() , ∵PQ⊥x轴时,运动停止,
, ∵PQ⊥x轴时,运动停止,
∴OH≤OQ, ∴m≤9-![]() ,且m≥0.
,且m≥0.
∴0≤m≤4.
(2)若OP=PQ,则OH=![]() OQ,∴m=
OQ,∴m=![]() (9-
(9-![]() ),m=
),m=![]() ,
,
若OP=OQ则![]() =9-
=9-![]() ,m=
,m=![]() .
.
∴m=![]() 或
或![]() .
.
(3) 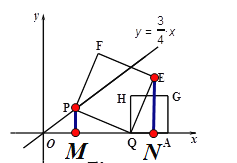
①易证PMQ≌QNE,∴QN=PM=![]() m,
m,
∴ON=OQ+QN
=9-![]() +
+![]() m
m
=9-![]() m
m
且EN=MQ=OQ-OM=9-![]() -m=9-
-m=9-![]()
∴E(9-![]() m,9-
m,9-![]() )
)
②易求F(![]() ,
,![]() ),
),
若点P在HQ上,则m=9-![]() ,m=4.
,m=4.
若点F在HG上,则![]() =
=![]() ,m=
,m=![]() .
.
若点F在AG上,则![]() =9,m=
=9,m=![]() .(舍)
.(舍)
若点E在HG上,则9-![]() =
=![]() ,m=
,m=![]() .
.
若点E在HG上,则9-![]() m=9,m=0(舍).
m=9,m=0(舍).
∴m=4, ![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为 cm2 .
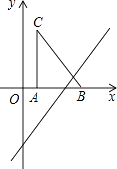
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)a2b-abc; (2)3a(x-y)+9(y-x);
(3)(2a-b)2+8ab; (4)(m2-m)2+
 (m2-m)+
(m2-m)+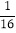 .
. -
科目: 来源: 题型:
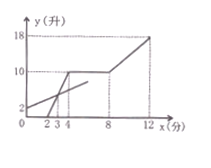
查看答案和解析>>【题目】现有甲、乙两个容器,分别装有进水管和出水管 ,两容器的进出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管。直到12分钟时,同时关闭两容器的进出水管。打开和关闭水管的时间忽略不计。容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示
(1)求甲容器的进、出水速度;
(2)当
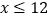 时,在这过程中是否存在两容器的水量相等?若存在,求出此时x的值;
时,在这过程中是否存在两容器的水量相等?若存在,求出此时x的值; (3)如果在乙容器中再装一个进水管,其进水速度是2升/分,若使两容器第12分钟时的水量相等 ,则应该在第几分钟打开此进水管?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,然后解答问题:
分解因式:x3+3x2-4.
解答:把x=1代入多项式x3+3x2-4,发现此多项式的值为0,由此确定多项式x3+3x2-4中有因式(x-1),于是可设x3+3x2-4=(x-1)(x2+mx+n),分别求出m,n的值,再代入x3+3x2-4=(x-1)(x2+mx+n),就容易分解多项式x3+3x2-4.这种分解因式的方法叫“试根法”.
(1)求上述式子中m,n的值;
(2)请你用“试根法”分解因式:x3+x2-16x-16.
-
科目: 来源: 题型:
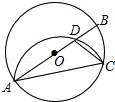
查看答案和解析>>【题目】如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数为度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,连接AD,AE.
(1)若∠BAC=110°,求∠DAE的度数;
(2)若∠BAC=θ(0°<θ<180°),求∠DAE的度数.(用含θ的式子表示)
相关试题

