【题目】小明在学习过程中遇到这样一个问题:
“一个木箱漂浮在河水中,随河水向下游漂去,在木箱上游和木箱下游各有一条小船,分别为甲船和乙船,两船距木箱距离相等,同时划向木箱,若两船在静水中划行的速度是30m/min,那么哪条小船先遇到木箱?”
小明是这样分析解决的:
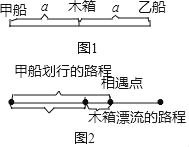
小明想通过比较甲乙两船遇见木箱的时间,知道哪条小船先遇见木箱.设甲船遇见木箱的时间为xmin,乙船遇见木箱的时间为ymin,开始时两船与木箱距离相等,都设为am,如图1.
如图2,利用甲船划行的路程﹣木箱漂流的路程=开始时甲船与木箱的距离:
列方程:x(30+5)﹣5x=a
解得,x=![]()
所以甲船遇见木箱的时间为![]() min.
min.
(1)参照小明的解题思路继续完成上述问题;
(2)借鉴小明解决问题的方法和(1)中发现的结论解决下面问题:
问题:“在一河流中甲乙两条小船,同时从A地出发,甲船逆流而上,乙船顺流而下;划行10分钟后,乙船发现船上木箱不知何时掉入水中,乙船立即通知甲船,两船同时掉头寻找木箱,若两船在静水中划行的速度是v(单位:m/min,v大于5),水流速度是5m/min,两船同时遇见木箱,那么木箱是出发几分钟后掉入水中的?”
参考答案:
【答案】(1)两船同时遇到木箱;(2)木箱是出发0分钟后掉入水中的.
【解析】
(1) 根据乙船划行的路程+木箱漂流的路程=开始时乙船与木箱的距离, 即可列出关于ッ的一元一次方程, 解之即可求出y值, 将x、 y值比较后即可得出结论;
(2) 设木箱是出发份分钟后掉入水中的, 根据(1) 可知10分钟时两船距离木箱的距离相等, 依此即可得出关于t的一元一次方程, 解之即可得出结论.
(1)利用乙船划行的路程+木箱漂流的路程=开始时乙船与木箱的距离:
列方程:y(30﹣5)+5y=a,
解得:y=![]()
∴乙船遇见木箱的时间为![]() min.
min.
∵![]() =
=![]() ,
,
∴两船同时遇到木箱.
(2)设木箱是出发t分钟后掉入水中的,
根据题意得:10(v﹣5)+(v+5)t+5(10﹣t)=v(10﹣t),
整理得:2vt=0,
解得:t=0.
答:木箱是出发0分钟后掉入水中的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2﹣bx+2(a≠0)图象的顶点在第二象限,且过点(1,0),则a的取值范围是;若a+b的值为非零整数,则b的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC.
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用棱长为a的小正方体拼成长方体,按照这样的拼法,第n个长方体表面积是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
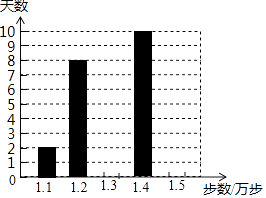
(1)若乐乐这个月平均每天健步走的步数为1.32万步,试求她走1.3万步和1.5万步的天数;
(2)求这组数据中的众数和中位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
3﹣
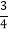 =3×
=3×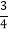 ;
;(﹣
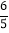 )﹣6=(﹣
)﹣6=(﹣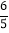 )×6;
)×6;(﹣0.5)﹣(﹣1)=(﹣0.5)×(﹣1)
根据上面这些等式反映的规律,解答下列问题:
(1)上面等式反映的规律用文字语言可以描述如下:存在两个有理数,使得这两个有理数的差等于
.
(2)若满足上述规律的两个有理数中有一个数是
 ,求另一个有理数;
,求另一个有理数;(3)若这两个有理数用字母a、b表示,则上面等式反映的规律用字母表示为 ;
(4)在(3)中的关系式中,字母a、b是否需要满足一定的条件?若需要,直接写出字母a、b应满足的条件;若不需要,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,M是等边△ABC边BC上的点,如图,连接AM,过点M作∠AMH=60°,MH与∠ACB的邻补角的平分线交于点H,过H作HD⊥BC于点D
(1)求证:MA=MH
(2)猜想写出CB、CM、CD之间的数量关系式,并加以证明.

相关试题

