【题目】已知,M是等边△ABC边BC上的点,如图,连接AM,过点M作∠AMH=60°,MH与∠ACB的邻补角的平分线交于点H,过H作HD⊥BC于点D
(1)求证:MA=MH
(2)猜想写出CB、CM、CD之间的数量关系式,并加以证明.

参考答案:
【答案】(1)见解析;(2)CB=CM+2CD.
【解析】(1)过M点作MN∥AC交AB于N,然后根据全等三角形的判定“ASA”证明△AMN≌△MHC,再根据全等三角形的性质可得MA=MH;
(2)过M点作MG⊥AB于G,再根据全等三角形的判定“AAS”证明△BMG≌△CHD可得CD=BG,因为BM=2CD可得BC=MC+2CD.
(1)如图,过M点作MN∥AC交AB于N,
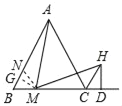
则BM=BN,∠ANM=120°,
∵AB=BC,
∴AN=MC,
∵CH是∠ACD的平分线,
∴∠ACH=60°=∠HCD,
∴∠MCH=∠ACB+∠ACH=120°,
又∵∠NMC=120°,∠AMH=60°,
∴∠HMC+∠AMN=60°
又∵∠NAM+∠AMN=∠BNM=60°,
∴∠HMC=∠MAN,
在△ANM和△MCH中,
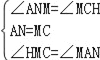 ,
,
∴△AMN≌△MHC(ASA),
∴MA=MH;
(2)CB=CM+2CD;
证明:如图,过M作MG⊥AB于G,
∵HD⊥BC,
∴∠HDC=∠MGB=90°,
∵△AMN≌△MHC,
∴MN=HC,
∵MN=MB,
∴HC=BM,
在△BMG和△CHD中,
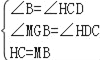 ,
,
∴△BMG≌△CHD(AAS),
∴CD=BG,
∵△BMN为等边三角形,
∴BM=2BG,
∴BM=2CD,
∴BC=MC+2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习过程中遇到这样一个问题:
“一个木箱漂浮在河水中,随河水向下游漂去,在木箱上游和木箱下游各有一条小船,分别为甲船和乙船,两船距木箱距离相等,同时划向木箱,若两船在静水中划行的速度是30m/min,那么哪条小船先遇到木箱?”
小明是这样分析解决的:
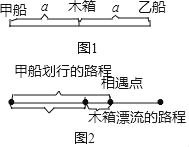
小明想通过比较甲乙两船遇见木箱的时间,知道哪条小船先遇见木箱.设甲船遇见木箱的时间为xmin,乙船遇见木箱的时间为ymin,开始时两船与木箱距离相等,都设为am,如图1.
如图2,利用甲船划行的路程﹣木箱漂流的路程=开始时甲船与木箱的距离:
列方程:x(30+5)﹣5x=a
解得,x=
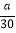
所以甲船遇见木箱的时间为
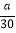 min.
min.(1)参照小明的解题思路继续完成上述问题;
(2)借鉴小明解决问题的方法和(1)中发现的结论解决下面问题:
问题:“在一河流中甲乙两条小船,同时从A地出发,甲船逆流而上,乙船顺流而下;划行10分钟后,乙船发现船上木箱不知何时掉入水中,乙船立即通知甲船,两船同时掉头寻找木箱,若两船在静水中划行的速度是v(单位:m/min,v大于5),水流速度是5m/min,两船同时遇见木箱,那么木箱是出发几分钟后掉入水中的?”
-
科目: 来源: 题型:
查看答案和解析>>【题目】乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
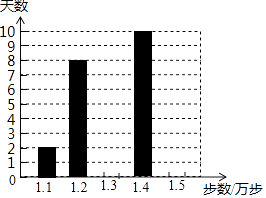
(1)若乐乐这个月平均每天健步走的步数为1.32万步,试求她走1.3万步和1.5万步的天数;
(2)求这组数据中的众数和中位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
3﹣
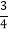 =3×
=3×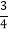 ;
;(﹣
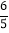 )﹣6=(﹣
)﹣6=(﹣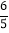 )×6;
)×6;(﹣0.5)﹣(﹣1)=(﹣0.5)×(﹣1)
根据上面这些等式反映的规律,解答下列问题:
(1)上面等式反映的规律用文字语言可以描述如下:存在两个有理数,使得这两个有理数的差等于
.
(2)若满足上述规律的两个有理数中有一个数是
 ,求另一个有理数;
,求另一个有理数;(3)若这两个有理数用字母a、b表示,则上面等式反映的规律用字母表示为 ;
(4)在(3)中的关系式中,字母a、b是否需要满足一定的条件?若需要,直接写出字母a、b应满足的条件;若不需要,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。

(1)求证:CE=CF。
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
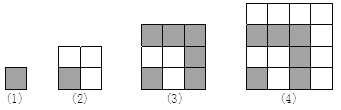 …
…第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形;
第(4)个图形有25小正方形;
……
(1)根据上面的发现我们可以猜想:1+3+5+7+…+(2n-1)的结果(用含n的代数式表示);
(2)请根据你的发现计算:① 1+3+5+7+…+99;
② 101+103+105+…+199.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过30立方米时,按2元/立方米计费;月用水量超过30立方米时,其中的30立方米仍按2元/立方米收费,超过部分按2.5元/立方米计费.设每户家庭月用水量为x立方米.
(1)当x不超过30时,应收多少水费(用x的代数式表示);当x超过30时,应收多少水费(用x的代数式表示);
(2)小明家四月份用水20立方米,五月份用水36立方米,请帮小明计算一下他家这两个月一共应交多少元水费?
相关试题

