搜索
【题目】如图，四幅图象分别表示变量之间的关系，请按图象的顺序，将下面的四种情境与之对应排序．正确的顺序是（ ）
①篮球运动员投篮时，投出去的篮球的高度与时间的关系
②去超市购买同一单价的水果，所付费用与水果数量的关系
③李老师使用的是一种含月租的手机计费方式，则他每月所付话费与通话时间的关系
④周末，小明从家到图书馆，看了一段时间书后，按原速度原路返回，小明离家的距离与时间的关系
A. ①②③④ B. ①③④② C. ①③②④ D. ①④②③
参考答案：
【答案】D
【解析】
反映了不同类别问题中，两个量的函数关系，按照问题与图象对号的方法，选择顺序．
①篮球运动员投篮时，投出去的篮球的高度与时间高应是抛物线形状，故①正确；
②去超市购买同一单价的水果，所付费用与水果数量的图象应先从0开始，变大，故④正确；
③李老师使用的是一种含月租的手机计费方式，则他每月所付话费与通话时间的应先从某一数值开始，变大，故②正确；
④周末，小明从家到图书馆，看了一段时间书后，按原速度原路返回，小明离家的距离与时间的图象由0开始，逐渐变大，而后不变，进而减小为0，故③正确；
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一列动车从甲地开往乙地，一列普通列车从乙地开往甲地，两车同时出发，设普通列车行驶的时间为
（小时），两车之间的距离为
（千米），图中的折线表示与之间的函数关系。根据图象回答下列问题：
（1）甲地与乙地相距______千米，两车出发后______小时相遇；
（2）普通列车到达终点共需_______小时，普通列车的速度是______千米/小时；
（3）动车的速度是________千米/小时；
（4）
的值为________. -
科目： 来源： 题型：
查看答案和解析>>【题目】我们已经知道，形如
的无理数的化简要借助平方差公式：例如：
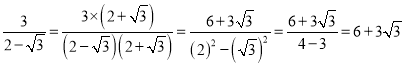。下面我们来看看完全平方公式在无理数化简中的作用。
问题提出：
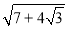该如何化简？建立模型：形如
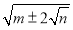的化简，只要我们找到两个数
，使
，这样
，
，那么便有：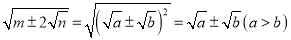
，问题解决：化简
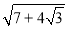，解：首先把
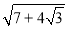化为
，这里
，
，由于4+3=7，
，即（
，
，∴
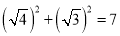模型应用1：
利用上述解决问题的方法化简下列各式：
（1）
；（2）
；模型应用2：
（3）在
中，
，
，
，那么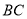
边的长为多少？（结果化成最简）。 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数
的图象分别与
轴和
轴交于
，
两点，且与正比例函数
的图象交于点
.
（1）求
的值；（2）求正比例函数的表达式；
（3）点
是一次函数图象上的一点，且
的面积是3，求点的坐标；（4）在
轴上是否存在点
，使
的值最小？若存在，求出点的坐标，若不存在，说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，E，F分别是AD，BC的中点，AF与BE相交于点M，CE与DF相交于点N，QM⊥BE，QN⊥EC相交于点Q，PM⊥AF，PN⊥DF相交于点P，若2BC=3AB，记△ABM和△CDN的面积和为S，则四边形MQNP的面积为（ ）
A.
S B. 
S C. 
S D. 
S -
科目： 来源： 题型：
查看答案和解析>>【题目】如下图，在平面直角坐标系中，对
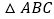进行循环往复的轴对称变换，若原来点A坐标是
，则经过第2019次变换后所得的A点坐标是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
中，
.⑴已知线段AB的垂直平分线与BC边交于点P，连结AP，求证：
；⑵以点B为圆心，线段AB的长为半径画弧，与BC边交于点Q，连结AQ，若
，求
的度数.
相关试题
