【题目】如图,AC是一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光直射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树高AC的高度(结果精确到0.1m,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
参考答案:
【答案】解:如图,过点D作DP⊥BE于点P,作DQ⊥AC于点Q,

∵∠DBP=30°、BD=4,
∴CQ=DP= ![]() BD=2,BP=BDcos∠DBP=4×
BD=2,BP=BDcos∠DBP=4× ![]() =2
=2 ![]() ,
,
则DQ=CP=BP+BC=2 ![]() +6,
+6,
∵太阳光直射斜坡BF,
∴∠ADB=90°
又∵∠QDB=∠DBP=30°,
∴∠ADQ=60°,
则AQ=DQtan∠ADQ=(2 ![]() +6)
+6) ![]() =6+6
=6+6 ![]() ,
,
∴树高AC=AQ+CQ=6+6 ![]() +2=8+6
+2=8+6 ![]() ≈18.4(m),
≈18.4(m),
答:树高AC的高度约为18.4m.
【解析】过点D作DP⊥BE于点P,作DQ⊥AC于点Q,∠DBP=30°、BD=4,CQ=DP= ![]() BD=2,BP=BDcos∠DBP,则DQ=CP=BP+BC,在Rt△ADQ中由解三角函数得出AQ=DQtan∠ADQ进而找到树高。
BD=2,BP=BDcos∠DBP,则DQ=CP=BP+BC,在Rt△ADQ中由解三角函数得出AQ=DQtan∠ADQ进而找到树高。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点P在∠AOB内,点M、N分别是点P关于AO、BO所在直线的对称点.
(1)若△PEF的周长为20,求MN的长.
(2)若∠O=50°,求∠EPF的度数.
(3)请直接写出∠EPF与∠O的数量关系是_____________________________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,且AB=6,C是⊙O上一点,D是
 的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连接AD.
的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连接AD.
(1)求证:AF⊥EF;
(2)填空:
①当BE=时,点C是AF的中点;
②当BE=时,四边形OBDC是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,
中, 厘米,
厘米, ,
,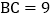 厘米,点D为AB的中点
厘米,点D为AB的中点 如果点P在线段BC上以v厘米
如果点P在线段BC上以v厘米 秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动
秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动 若点Q的运动速度为3厘米
若点Q的运动速度为3厘米 秒,则当
秒,则当 与
与 全等时,v的值为
全等时,v的值为

A.
 B. 3 C.
B. 3 C.  或3 D. 1或5
或3 D. 1或5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β;②α-β;③β-α;④180°-α-β中.∠AEC的度数可能是 _____(把正确答案的序号填在横线上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行“建国70周年”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如下不完整的两幅统计图表.


请根指以上信息,解答下列问题
(1)征文比赛成绩频数分布表中,a= ,b= ,c= .
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
相关试题

