【题目】正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒1 cm,乙的速度为每秒5 cm,已知正方形轨道ABCD的边长为2 cm,则乙在第2 020次追上甲时的位置在( )

A.AB上B.BC上
C.CD上D.AD上
参考答案:
【答案】D
【解析】
根据题意列一元一次方程,然后四个循环为一次即可求得结论.
解:设乙走x秒第一次追上甲.
根据题意,得
5x-x=4
解得x=1.
∴乙走1秒第一次追上甲,则乙在第1次追上甲时的位置是AB上;
设乙再走y秒第二次追上甲.
根据题意,得5y-y=8,解得y=2.
∴乙再走2秒第二次追上甲,则乙在第2次追上甲时的位置是BC上;
同理:∴乙再走2秒第三次次追上甲,则乙在第3次追上甲时的位置是CD上;
∴乙再走2秒第四次追上甲,则乙在第4次追上甲时的位置是DA上;
乙在第5次追上甲时的位置又回到AB上;
∴2020÷4=505
∴乙在第2020次追上甲时的位置是AD上.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x轴交于A(-1,0),B(4,0),与y轴交于C(0,-2).(1)求抛物线的解析式;
(2)H是C关于x轴的对称点,P是抛物线上的一点,当△PBH与△AOC相似时,求符合条件的P点的坐标(求出两点即可);
(3)过点C作CD∥AB,CD交抛物线于点D,点M是线段CD上的一动点,作直线MN与线段AC交于点N,与x轴交于点E,且∠BME=∠BDC,当CN的值最大时,求点E的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】新定义函数:在y关于x的函数中,若0≤x≤1时,函数y有最大值和最小值,分别记ymax和ymin,且满足
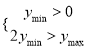 ,则我们称函数y为“三角形函数”.
,则我们称函数y为“三角形函数”.(1)若函数y=x+a为“三角形函数”,求a的取值范围;
(2)判断函数y=x2﹣
 x+1是否为“三角形函数”,并说明理由;
x+1是否为“三角形函数”,并说明理由;(3)已知函数y=x2﹣2mx+1,若对于0≤x≤1上的任意三个实数a,b,c所对应的三个函数值都能构成一个三角形的三边长,则求满足条件的m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂第一季度的电费为
 元,水费比电费的2倍多40元。第二季度电费比第一季度节约了25%,水费比第一季度多支出了25%。问该工厂第一季度、第二季度的水电费为多少元?第二季度的水电费与第一季度相比是超支还是节约了?超支或节约了多少元?
元,水费比电费的2倍多40元。第二季度电费比第一季度节约了25%,水费比第一季度多支出了25%。问该工厂第一季度、第二季度的水电费为多少元?第二季度的水电费与第一季度相比是超支还是节约了?超支或节约了多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数
 (k≠0)的图象过点C,则该反比例函数的表达式为( )
(k≠0)的图象过点C,则该反比例函数的表达式为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于
 PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为_____.
PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在长方形
 中,
中, 点在
点在 上,并且
上,并且 ,分别以
,分别以 、
、 为折痕进行折叠并压平,如图②,若图②中
为折痕进行折叠并压平,如图②,若图②中 ,则
,则 的度数为______度.
的度数为______度.
相关试题

