【题目】如图,在ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于![]() PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为_____.
PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为_____.

参考答案:
【答案】2
【解析】根据作图过程可得得AE平分∠ABC;再根据角平分线的性质和平行四边形的性质可证明∠AEB=∠CBE,证出AE=AB=3,即可得出DE的长.,
解:根据作图的方法得:AE平分∠ABC,
∴∠ABE=∠CBE
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=3,
∴DE=AD﹣AE=5﹣3=2;
故答案为:2.
“点睛”此题考查了平行四边形的性质、等腰三角形的判定.熟练掌握平行四边形的性质,证出AE=AB是解决问题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△ABC,∠A=40°,∠B=110°,则∠C=( ).
A.40°
B.110°
C.70°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
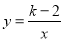 的图象如图2,则一元二次
的图象如图2,则一元二次方程
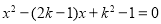 根的情况是( )
根的情况是( )A.有两个不等实根B.有两个相等实根
C.没有实根 D.无法确定。
-
科目: 来源: 题型:
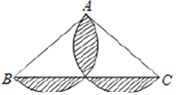
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是为________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,DE垂直平分AC , DF⊥BC , 当△ABC满足条件时,四边形DECF是正方形.(要求:①不再添加任何辅助线,②只需填一个符合要求的条件)

-
科目: 来源: 题型:
查看答案和解析>>【题目】去括号正确的是( )
A.﹣(2a+b﹣c)=2a+b﹣c
B.﹣2(a+b﹣3c)=﹣2a﹣2b+6c
C.﹣(﹣a﹣b+c)=﹣ab+c
D.﹣(a﹣b﹣c)=﹣a+b﹣c -
科目: 来源: 题型:
查看答案和解析>>【题目】有13位同学参加学校组织的才艺表演比赛,已知他们所得的分数互不相同,共设7个获奖名额,某同学知道自己的比赛分数后,要判断自己能否获奖,在这13名同学成绩的统计量中只需知道一个量,它是____.(填“众数”“方差”“中位数”或“平均数”)
相关试题

