Question

【题目】新定义函数：在y关于x的函数中，若0≤x≤1时，函数y有最大值和最小值，分别记ymax和ymin，且满足，则我们称函数y为“三角形函数”．

（1）若函数y=x+a为“三角形函数”，求a的取值范围；

（2）判断函数y=x2﹣x+1是否为“三角形函数”，并说明理由；

（3）已知函数y=x2﹣2mx+1，若对于0≤x≤1上的任意三个实数a，b，c所对应的三个函数值都能构成一个三角形的三边长，则求满足条件的m的取值范围．

Answer 1

【答案】(1) a＞1(2)是(3)0<m 或<m<

【解析】试题分析：（1）由函数的性质可求得其最大值和最小值，由三角形函数的定义可得到关于a的不等式组，可求得a的取值范围；
（2）由抛物线解析式可求得其对称轴，由x的范围可求得其最大值和最小值，满足三角形函数的定义；
（3）由三角形的三边关系可判断函数y=x2-2mx+1为三角形函数，再利用三角形函数的定义分别得到关于m的不等式组，即可求得m所满足的不等式，可求得m的取值范围．

试题解析：（1）∵当x=0，ymin=a；x=1，ymax=1+a，

∵y=x+a为三角形函数，

∴，

∴a＞1；

（2）是三角形函数，理由如下：

∵对称轴为直线，0≤x≤1，

∴当，

∴，

∴它是三角形函数；

（3）∵对于0≤x≤1上的任意三个实数a，b，c所对应的三个函数值都能构成一个三角形的三边长，

∴，若a为最小，c为最大，则有，同理当b为最小，c为最大时也可得，

∴y=x2﹣2mx+1是三角形函数，

∵y=x2﹣2mx+1=（x﹣m）2﹣m2+1，

∴对称轴为直线x=m，

①当m≤0时，当x=0，ymin=1，

当x=1，ymax=﹣2m+2，则2＞﹣2m+2，解得m＞0，

∴无解；

②当，，当x=1，ymax=﹣2m+2，，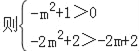

解得0＜m＜1，

∴；

③当，，当x=0，ymax=1，则，

解得，

∴；

④当m＞1，当x=1，ymin=﹣2m+2，x=0，ymax=1，则，

解得，

∴无解；

综上述可知m的取值范围为或．