【题目】如图所示,左边的正方形与右边的扇形面积相等,扇形的半径和正方形的边长都是2cm,则此扇形的弧长为( )cm.
A.4
B.4π
C.8
D.8﹣π
参考答案:
【答案】A
【解析】解:设扇形的圆心角为n.
由题意 ![]() =4,
=4,
∴n= ![]() ,
,
∴扇形的弧长为= ![]() =4cm,
=4cm,
故A符合题意.
所以答案是:A.
【考点精析】本题主要考查了正方形的性质和弧长计算公式的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了
 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着 展开式中的系数等等.
展开式中的系数等等.
(1)根据上面的规律,写出
 的展开式.
的展开式.(2)利用上面的规律计算:

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了保护环境,某化工厂一期工程完成后购买了
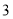 台甲型和
台甲型和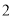 台乙型污水处理设备,共花费资金
台乙型污水处理设备,共花费资金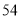 万元,且每台乙型设备的价格是每台甲型设备价格的
万元,且每台乙型设备的价格是每台甲型设备价格的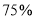 ,实际运行中发现,每台甲型设备每月能处理污水
,实际运行中发现,每台甲型设备每月能处理污水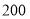 吨,每台乙型设备每月能处理污水
吨,每台乙型设备每月能处理污水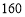 吨.今年该厂二期工程即将完成产生的污水将大大增加,于是该厂决定再购买甲、乙两种型号设备共
吨.今年该厂二期工程即将完成产生的污水将大大增加,于是该厂决定再购买甲、乙两种型号设备共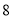 台用于二期工程的污水处理,预算本次购买资金不超过
台用于二期工程的污水处理,预算本次购买资金不超过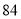 万元,预计二期工程完成后每月将产生不少于
万元,预计二期工程完成后每月将产生不少于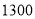 吨污水.
吨污水.(1)请你计算每台甲型设备和每台乙型设备的价格各是多少元;
(2)请你求出用于二期工程的污水处理设备的所有购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,AD=8,点E在BC边上,且BE:EC=1:3.动点P从点B出发,沿BA运动到点A停止.过点E作EF⊥PE交边AD或CD于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出:
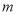 ,
,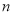 分别是什么数时,多项式
分别是什么数时,多项式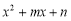 和
和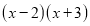 恒等?
恒等?阅读理解:
所谓恒等式,就是指不论用任何数值来代替式中的变量,左、右两边的值都相等的等式.我们用符号“
 ”来表示恒等,读作“恒等于”.于是,上面的问题也可以表述为:已知
”来表示恒等,读作“恒等于”.于是,上面的问题也可以表述为:已知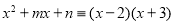 ,求待定系数
,求待定系数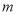 ,
,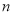 .
.问题解决:
(方法1—数值代入法)由恒等式的概念,我们每用一个数值来代替问题中的
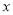 ,即可得到一个关于
,即可得到一个关于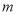 与
与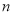 的方程.因此,要求出
的方程.因此,要求出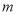 与
与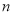 的值,只需要用两个不同的数值分别代替式中的
的值,只需要用两个不同的数值分别代替式中的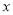 ,就可以得到一个关于
,就可以得到一个关于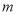 与
与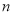 的二元一次方程组,解这个方程组,即可求得
的二元一次方程组,解这个方程组,即可求得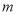 与
与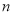 .
.解:分别用
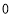 ,
,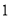 代替式中的
代替式中的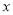 ,得
,得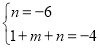
解之,得
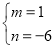
(方法2—系数比较法)
定理 如果
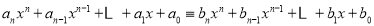 ,
,那么
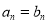 ,
,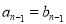 ,
, ,
,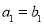 ,
,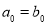 .
.根据这个定理,也可以这样解:
解:由题设
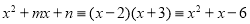 ,
,比较对应项的系数,得
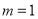 ,
,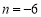 .
.请回答下面的问题:
(1)已知多项式
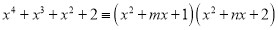 .求
.求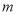 与
与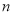 的值;
的值;(2)如果
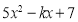 被
被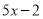 除后余
除后余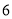 ,求
,求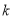 的值及商式.
的值及商式. -
科目: 来源: 题型:
查看答案和解析>>【题目】防疫期间的某天上午9:00,社区工作人员小孙从社区办公室出发,上门为本社区两户隔离人员家庭送生活用品,同时了解隔离人员的健康状况,她先去了距离社区较近的张家,稍作停留简单询问了情况后,又去了稍远一点的李家,这家人口较多,了解情况时间稍长一些,由于社区还有其它事情等待处理,结束工作后她快速返回社区办公室.已知小孙距离社区办公室的距离
 (米)与离开办公室的时间
(米)与离开办公室的时间 (分)之间的关系如图所示.请根据图象回答下列问题:
(分)之间的关系如图所示.请根据图象回答下列问题:
(1)图中
 点表示的意义是什么?
点表示的意义是什么?(2)小孙从李家出来后步行的速度是多少?
(3)小孙在李家停留了几分钟?小孙几点回到社区办公室?
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求完成下列推理证明.
如图,已知点D为BC延长线上一点,CE∥AB.
求证:∠A+∠B+∠ACB=180°

证明:∵CE∥AB,
∴∠1= ,( )
∠2= ,( )
又∠1+∠2+∠ACB=180°(平角的定义),
∴∠A+∠B+∠ACB=180°
相关试题

