【题目】按要求完成下列推理证明.
如图,已知点D为BC延长线上一点,CE∥AB.
求证:∠A+∠B+∠ACB=180°

证明:∵CE∥AB,
∴∠1= ,( )
∠2= ,( )
又∠1+∠2+∠ACB=180°(平角的定义),
∴∠A+∠B+∠ACB=180°
参考答案:
【答案】∠B;两直线平行,同位角相等;∠A;两直线平行,内错角相等.
【解析】
根据平行线的性质得出∠1=∠B,∠2=∠A,即可得出答案.
证明:∵CE∥AB,
∴∠1=∠B,( 两直线平行,同位角相等)
∠2=∠A,(两直线平行,内错角相等)
又∠1+∠2+∠ACB=180°(平角的定义),
∴∠A+∠B+∠ACB=180°,
故答案为:∠B;两直线平行,同位角相等;∠A;两直线平行,内错角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,左边的正方形与右边的扇形面积相等,扇形的半径和正方形的边长都是2cm,则此扇形的弧长为( )cm.

A.4
B.4π
C.8
D.8﹣π -
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出:
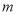 ,
,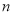 分别是什么数时,多项式
分别是什么数时,多项式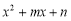 和
和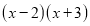 恒等?
恒等?阅读理解:
所谓恒等式,就是指不论用任何数值来代替式中的变量,左、右两边的值都相等的等式.我们用符号“
 ”来表示恒等,读作“恒等于”.于是,上面的问题也可以表述为:已知
”来表示恒等,读作“恒等于”.于是,上面的问题也可以表述为:已知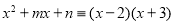 ,求待定系数
,求待定系数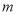 ,
,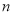 .
.问题解决:
(方法1—数值代入法)由恒等式的概念,我们每用一个数值来代替问题中的
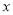 ,即可得到一个关于
,即可得到一个关于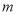 与
与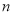 的方程.因此,要求出
的方程.因此,要求出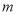 与
与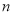 的值,只需要用两个不同的数值分别代替式中的
的值,只需要用两个不同的数值分别代替式中的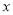 ,就可以得到一个关于
,就可以得到一个关于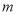 与
与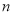 的二元一次方程组,解这个方程组,即可求得
的二元一次方程组,解这个方程组,即可求得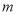 与
与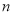 .
.解:分别用
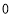 ,
,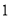 代替式中的
代替式中的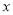 ,得
,得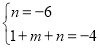
解之,得
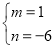
(方法2—系数比较法)
定理 如果
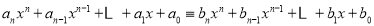 ,
,那么
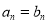 ,
,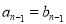 ,
, ,
,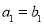 ,
,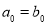 .
.根据这个定理,也可以这样解:
解:由题设
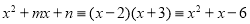 ,
,比较对应项的系数,得
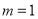 ,
,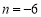 .
.请回答下面的问题:
(1)已知多项式
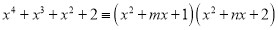 .求
.求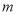 与
与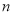 的值;
的值;(2)如果
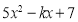 被
被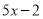 除后余
除后余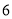 ,求
,求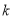 的值及商式.
的值及商式. -
科目: 来源: 题型:
查看答案和解析>>【题目】防疫期间的某天上午9:00,社区工作人员小孙从社区办公室出发,上门为本社区两户隔离人员家庭送生活用品,同时了解隔离人员的健康状况,她先去了距离社区较近的张家,稍作停留简单询问了情况后,又去了稍远一点的李家,这家人口较多,了解情况时间稍长一些,由于社区还有其它事情等待处理,结束工作后她快速返回社区办公室.已知小孙距离社区办公室的距离
 (米)与离开办公室的时间
(米)与离开办公室的时间 (分)之间的关系如图所示.请根据图象回答下列问题:
(分)之间的关系如图所示.请根据图象回答下列问题:
(1)图中
 点表示的意义是什么?
点表示的意义是什么?(2)小孙从李家出来后步行的速度是多少?
(3)小孙在李家停留了几分钟?小孙几点回到社区办公室?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两条直线
 ,
, 相交.
相交.
(1)如果
 ,求
,求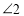 ,
, 的度数;
的度数;(2)如果
 ,求
,求 ,
, 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若 =
=  ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH . 
A.1个
B.2个
C.3个
D.4个
相关试题

