搜索
【题目】如图1，已知点E，F，G，H是矩形ABCD各边的中点，AB=6，BC=8，动点M从点E出发，沿E→F→G→H→E匀速运动，设点M运动的路程x，点M到矩形的某一个顶点的距离为y，如果表示y关于x函数关系的图象如图2所示，那么这个顶点是矩形的（ ）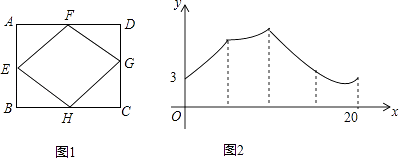
A.点A
B.点B
C.点C
D.点D
参考答案：
【答案】B
【解析】解：由图2得出始点E到顶点的距离为3，
∵AB=6，
∴只有顶点A，B满足，
又∵沿E→F→G→H→E匀速运动开始时先增大，
∴只有顶点B满足，
故选：B．
【考点精析】关于本题考查的函数的图象，需要了解函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，直线y=﹣
x+4与x轴、y轴分别交于点A、点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．（1）求AB的长和点C的坐标；
（2）求直线CD的解析式；
（3）y轴上是否存在一点P，使得S△PAB=
，若存在，请求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料： 小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：
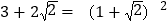，善于思考的小明进行了以下探索：设
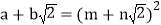（其中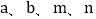
均为整数），则有
．∴
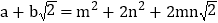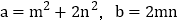．这样小明就找到了一种把部分
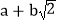的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：
当
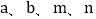均为正整数时，若
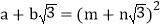，用含m、n的式子分别表示
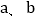，得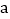
＝ ，
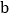＝ ；（2）利用所探索的结论，找一组正整数
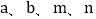，填空： ＋ ＝( ＋ 
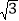)2；（3）若
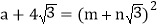，且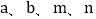均为正整数，求的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读以下材料：
对数的创始人是苏格兰数学家纳皮尔（J．Nplcr，1550﹣1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evlcr，1707﹣1783年）才发现指数与对数之间的联系．
对数的定义：一般地，若ax=N（a＞0，a≠1），那么x叫做以a为底N的对数，记作：x=logaN．比如指数式24=16可以转化为4=log216，对数式2=log525可以转化为52=25．
我们根据对数的定义可得到对数的一个性质：loga（MN）=logaM+logaN（a＞0，a≠1，M＞0，N＞0）；理由如下：
设logaM=m，logaN=n，则M=am，N=an
∴MN=aman=am+n，由对数的定义得m+n=loga（MN）
又∵m+n=logaM+logaN
∴loga（MN）=logaM+logaN
解决以下问题：
（1）将指数43=64转化为对数式_____；
（2）证明loga
=logaM﹣logaN（a＞0，a≠1，M＞0，N＞0）（3）拓展运用：计算log32+log36﹣log34=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有一个面积为1的正方形，经过一次“生长”后，在它的左右肩上生出两个小正方形，如图①，其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了图②，如果继续“生长”下去 ，它将变得“枝繁叶茂”，则“生长”了2 014次后形成的图形中所有正方形的面积和是( )
A. 2 012 B. 2 013 C. 2 014 D. 2 015
-
科目： 来源： 题型：
查看答案和解析>>【题目】中国国家邮政局公布的数据显示，2016年中国快递业务量突破313.5亿件，同比增长51.7%，快递业务量位居世界第一，业内人士表示，快递业务连续6年保持50%以上的高速增长，已成为中国经济的一匹“黑马”，未来中国快递业务仍将保持快速增长势头，以下是根据相关数据绘制的统计图，请你预估2017年全国快递的业务量大约为（精确的0.1）亿元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：（
）﹣1+tan60°+|﹣ 
|﹣ 
．
相关试题
