【题目】A、B两地相距60km,甲从A地去B地,乙从B地去A地,图中![]() 、
、![]() 分别表示甲、乙两人到B地的距离y(km)与甲出发时间x(h)的函数关系图象.
分别表示甲、乙两人到B地的距离y(km)与甲出发时间x(h)的函数关系图象.
(1)根据图象,求乙的行驶速度.
(2)解释交点A的实际意义.
(3)求甲出发多少时间,两人之间恰好相距5km?


参考答案:
【答案】(1)答案见解析;(2)答案见解析;(3)答案见解析.
【解析】
(1)由图像得知乙从B地去A地共用3小时,从而求乙的速度;(2)根据函数图象中的数据可以求出点A的坐标,并说出点A的实际意义;(3)根据(1)中的函数解析式,可以列出相应的等式,从而可以求得甲出发多少时间,两人之间的距离恰好相距5km.
解:(1)由图象可得,
乙的行驶速度为:60÷(3.5-0.5)=20km/h,
(2)设l1对应的函数解析式为y1=k1x+b1,把(0,60)(2,0)代入得: ,得
,得 ,
,
即l1对应的函数解析式为y1=-30x+60,
设l2对应的函数解析式为y2=k2x+b2,把(0.5,0)(3.5,60)代入得: ,得
,得 ,
,
即l2对应的函数解析式为y2=20x-10,
∴![]() ,得
,得![]() ,
,
即点A的坐标为(1.4,18),
∴点A的实际意义是在甲出发1.4小时时,甲乙两车相遇,此时距离B地18km;(3)由题意可得,
当![]() 时(-30x+60)-(20x-10)=5,解得x=1.3
时(-30x+60)-(20x-10)=5,解得x=1.3
当![]() 时,(20x-10)-(-30x+60)=5,解得x=1.5
时,(20x-10)-(-30x+60)=5,解得x=1.5
答:当甲出发1.3h或1.5h时,两人之间的距离恰好相距5km;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解该校七年级学生的身高情况,抽样调查了部分同学身高,将所得数据处理后,制成扇形统计图和频数分布直方图(部分)如下(每组只含最低值不含最高值,身高单位:cm,测量时精确到1cm):
(1)请根据所提供的信息补全频数分布直方图;
(2)样本的中位数落在 (身高值)段中;
(3)如果该校七年级共有500名学生,那么估计全校身高在160cm或160cm以上的七年级学生有 人;
(4)如果上述七年级样本的平均数为157cm,方差为0.8;该校八年级学生身高的平均数为159cm,方差为0.6,那么 学生的身高比较整齐.(填“七年级”或“八年级”)

-
科目: 来源: 题型:
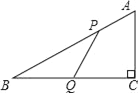
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AB=10,BC=8,P、Q分别是AB、BC边上的点,且AP=BQ=a (其中0<a<8).
(1)若PQ⊥BC,求a的值;
(2)若PQ=BQ,把线段CQ绕着点Q旋转180°,试判别点C的对应点C’是否落在线段QB上?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为
 ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=ax2+4x+c(a≠0)经过点A(3,﹣4)和B(0,2).
(1)求抛物线的表达式和顶点坐标;
(2)将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿直线x=3翻折,得到图象N.若过点C(9,4)的直线y=kx+b与图象M、图象N都相交,且只有两个交点,求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求
 的值.
的值.(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的
 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
相关试题

