【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求![]() 的值.
的值.
(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的![]() 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
参考答案:
【答案】(1)△ABC是“等高底”三角形;(2)![]() ;(3)CD的值为
;(3)CD的值为![]() ,2
,2![]() ,2.
,2.
【解析】
(1)过A作AD⊥BC于D,则△ADC是直角三角形,∠ADC=90°,根据30°所对的直角边等于斜边的一半可得:![]() 根据“等高底”三角形的概念即可判断.
根据“等高底”三角形的概念即可判断.
(2)点B是![]() 的重心,得到
的重心,得到![]() 设
设![]() 则
则![]()
根据勾股定理可得![]() 即可求出它们的比值.
即可求出它们的比值.
(3)分两种情况进行讨论:①当![]() 时和②当
时和②当![]() 时.
时.
(1)△ABC是“等高底”三角形;
理由:如图1,过A作AD⊥BC于D,则△ADC是直角三角形,∠ADC=90°,

∵∠ACB=30°,AC=6,
∴![]()
∴AD=BC=3,
即△ABC是“等高底”三角形;
(2)如图2,∵△ABC是“等高底”三角形,BC是“等底”,

∴![]()
∵△ABC关于BC所在直线的对称图形是![]() ,
,
∴∠ADC=90°,
∵点B是![]() 的重心,
的重心,
∴![]()
设![]() 则
则![]()
由勾股定理得![]()
∴![]()
(3)①当![]() 时,
时,
Ⅰ.如图3,作AE⊥BC于E,DF⊥AC于F,
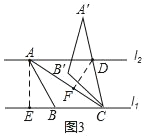
∵“等高底”△ABC的“等底”为BC,l1∥l2,l1与l2之间的距离为2,![]() .
.
∴![]()
∴BE=2,即EC=4,
∴![]()
∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,
∴∠DCF=45°,
设![]()
∵l1∥l2,
∴![]()
∴![]() 即
即![]()
∴![]()
∴![]()
Ⅱ.如图4,此时△ABC等腰直角三角形,

∵△ABC绕点C按顺时针方向旋转45°得到![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]()
②当![]() 时,
时,
Ⅰ.如图5,此时△ABC是等腰直角三角形,
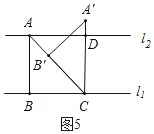
∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,
∴![]()
∴![]()
Ⅱ.如图6,作![]() 于E,则
于E,则![]()
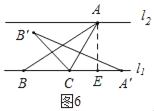
∴![]()
∴![]()
∴△ABC绕点C按顺时针方向旋转45°,得到![]() 时,点A'在直线l1上,
时,点A'在直线l1上,
∴![]() ∥l2,即直线
∥l2,即直线![]() 与l2无交点,
与l2无交点,
综上所述,CD的值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距60km,甲从A地去B地,乙从B地去A地,图中
 、
、 分别表示甲、乙两人到B地的距离y(km)与甲出发时间x(h)的函数关系图象.
分别表示甲、乙两人到B地的距离y(km)与甲出发时间x(h)的函数关系图象.(1)根据图象,求乙的行驶速度.
(2)解释交点A的实际意义.
(3)求甲出发多少时间,两人之间恰好相距5km?


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=ax2+4x+c(a≠0)经过点A(3,﹣4)和B(0,2).
(1)求抛物线的表达式和顶点坐标;
(2)将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿直线x=3翻折,得到图象N.若过点C(9,4)的直线y=kx+b与图象M、图象N都相交,且只有两个交点,求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个商人要建一个矩形的仓库,仓库的两边是住房墙,另外两边用
 长的建筑材料围成,且仓库的面积为
长的建筑材料围成,且仓库的面积为 .
. 求这矩形仓库的长;
求这矩形仓库的长; 有规格为
有规格为 和
和 (单位:
(单位: )的地板砖单价分别为
)的地板砖单价分别为 元/块和
元/块和 元/块,若只选其中一种地板砖都恰好能铺满仓库的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
元/块,若只选其中一种地板砖都恰好能铺满仓库的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距 千米.
(2)B出发后 小时与A相遇.
(3)B走了一段路后,自行车发生故障,进行 修理,所用的时间是 小时.
(4)若B的自行车不发生故障,保持出发时的速度前进, 小时与A相遇,相遇点离B的出发点 千米.在图中表示出这个相遇点C.
(5)求出A行走的路程S与时间t的函数关系式.(写出过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解学生到校交通方式情况,随机抽取各年级部分学生就“上下学交通方式”进行问卷调查,调查分为“A:骑自行车;B:步行;C:坐公交车;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图①)和部分扇形统计图(如图②),请根据图中的信息,解答下列问题.
(1)本次调查共抽取 名学生;
(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(3)若该中学共有学生3000人,估计有多少学生在上下学交通方式中选择坐公交车?

相关试题

