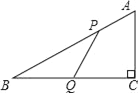
【题目】如图,在△ABC中,∠C=90°,AB=10,BC=8,P、Q分别是AB、BC边上的点,且AP=BQ=a (其中0<a<8).
(1)若PQ⊥BC,求a的值;
(2)若PQ=BQ,把线段CQ绕着点Q旋转180°,试判别点C的对应点C’是否落在线段QB上?请说明理由.
参考答案:
【答案】(1)![]() (2)点C′不落在线段QB上
(2)点C′不落在线段QB上
【解析】试题分析: (1)∵∠B=∠B,∠PQB=∠C=90°∴△BQP∽△BCA,
∴![]() ,
,![]() ,解得:a=
,解得:a=![]() ,
,
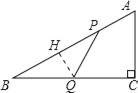
(2) 作QH⊥AB于H,∵PQ=BQ,∴BH=HP,∵∠B=∠B,∠BHQ=∠C,∴△BQH∽△BAC,
∴BH:BC=BQ:AB可得: ![]() (10﹣a):a=8:10,解得a=
(10﹣a):a=8:10,解得a=![]() ,CQ=(8﹣a)=
,CQ=(8﹣a)=![]() ,
,
∴BQ<QC,∴点C′不落在线段QB上.
试题解析:(1)∵∠B=∠B,∠PQB=∠C=90°
∴△BQP∽△BCA,
∴![]() ,
,![]() ,
,
解得:a=![]() ,
,
(2)点C′不落在线段QB上,
作QH⊥AB于H,
∵PQ=BQ,
∴BH=HP,
∵∠B=∠B,∠BHQ=∠C,
∴△BQH∽△BAC,
∴BH:BC=BQ:AB可得: ![]() (10﹣a):a=8:10,
(10﹣a):a=8:10,
解得a=![]() ,
,
CQ=(8﹣a)=![]() ,
,
∴BQ<QC,
∴点C′不落在线段QB上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.
其中正确结论的序号是( )

A. ①②③④⑤ B. ①②③④ C. ①③④⑤ D. ①④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中一个正方形剪开得到图③,图③中共有7个正方形;将图③中一个正方形剪开得到图④,图④中共有10个正方形…,如此下去,则第2014个图中共有正方形的个数为( )
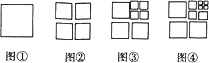
A. 2014. B. 2017 C. 6040 D. 6044
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2
 cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从
 两地同时出发,甲车匀速前往
两地同时出发,甲车匀速前往 地,到达
地,到达 地立即以另一速度按原路匀速返回到
地立即以另一速度按原路匀速返回到 地;乙车匀速前往
地;乙车匀速前往 地,设甲、乙两车距
地,设甲、乙两车距 地的路程为
地的路程为 (千米),甲车行驶的时间为
(千米),甲车行驶的时间为 (小时)
(小时) 与
与 之间的函数图象如图所示:
之间的函数图象如图所示:
(1)甲车从
 地开往
地开往 地时的速度是_________;乙车从
地时的速度是_________;乙车从 地开往
地开往 地时的速度是______.
地时的速度是______.(2)图中点
 的坐标是(______,______);
的坐标是(______,______);(3)求甲车返回时
 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.
(1)用代数式表示这两个篮球场的占地面积.
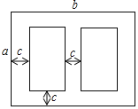
(2)当a=30,b=40,c=3时,计算出一个篮球场的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱.各种品牌的山地车相继投放市场.顺风车行经营的
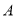 型车2018年6月份销售总额为
型车2018年6月份销售总额为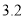 万元,今年经过改造升级后
万元,今年经过改造升级后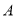 型车每辆销售价比去年增加
型车每辆销售价比去年增加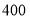 元,若今年6月份与去年6月份卖出的
元,若今年6月份与去年6月份卖出的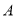 型车数量相同,则今年6月份
型车数量相同,则今年6月份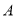 型车销售总额将比去年6月份销售总额增加
型车销售总额将比去年6月份销售总额增加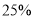 .
.(1)今年6月份
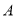 型车每辆售价多少元?(用列方程的方法解答)
型车每辆售价多少元?(用列方程的方法解答)(2)已知
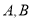 两种型号车今年的进货及销售价格如下表:
两种型号车今年的进货及销售价格如下表: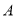 型车
型车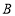 型车
型车进货价格(元/辆)
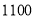
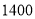
销售价格(元/辆)
今年的销售价格
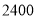
该车行计划7月份进这批
 型车和
型车和 型车共
型车共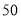 辆,且
辆,且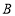 型车的进货数量不超过
型车的进货数量不超过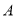 型车数量的两倍,应如何进货才能是这批车获利最多?
型车数量的两倍,应如何进货才能是这批车获利最多?
相关试题

