【题目】证明:两条平行线被第三条直线所截,一组同位角的平分线互相平行.

已知:如图,_______________________.
求证:_____________________________.
证明:
参考答案:
【答案】见解析
【解析】
根据题意画出图形,写出已知与求证,证明过程为:由AM与BN平行,利用两直线平行同位角相等得到一对角相等,再由AE与BF为角平分线,利用角平分线定义及等量代换得到一对同位角相等,利用同位角相等两直线平行可得出AE与BF平行,得证.
已知,AM∥BN,AE为∠CAM的平分线,BF为∠ABN的平分线,如图所示,

求证:AE∥BF.
证明:∵AM∥BN(已知),
∴∠CAM=∠ABN(两直线平行同位角相等),
∵AE为∠CAM的平分线,BF为∠ABN的平分线(已知),
∴∠CAE=![]() ∠CAM,∠ABF=
∠CAM,∠ABF=![]() ∠ABN(角平分线定义),
∠ABN(角平分线定义),
∴∠CAE=∠ABF(等量代换),
∴AE∥BF(同位角相等两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=4,BC=3,点P从点A出发,以每秒4个单位长度的速度沿折线AC-CB运动,到点B停止.当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB 于点Q,再以PQ为斜边作等腰直角三角形△PQR,且点R与△ABC的另一条直角边始终在PQ同侧,设△PQR与△ABC重叠部分图形的面积为S(平方单位).点P的运动时间为t(秒).
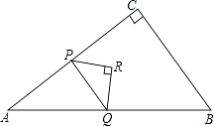
(1)求点P在AC边上时PQ的长,(用含t的代数式表示);
(2)求点R到AC、PQ所在直线的距离相等时t的取值范围;
(3)当点P在AC边上运动时,求S与t之间的函数关系式;
(4)直接写出点R落在△ABC高线上时t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;
Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:

则正确的配对是( )
A. ①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ B. ①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C. ①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ D. ①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“数学晚会”上,七年级的10个同学藏在10个大盾牌后面,男同学盾牌前面的结果是一个正数,女同学盾牌前面的结果是一个负数,这10个盾牌如图所示,请你通过计算,求出盾牌后面男、女同学各有多少人.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进甲,乙两种商品,若购买6件甲商品和3件乙商品共用108元;若购买5件甲商品和2件乙商品共用88元.
(1)求甲,乙两种商品每件的价格;
(2)已知该商店购买乙商品的件数比购买甲商品的件数多8件,如果需要购买甲,乙两种商品的总件数不少于32件,且商店购买的甲、乙两种商品的总费用不超过292元,那么该商店有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
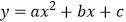 的图象如图所示,反比例函数
的图象如图所示,反比例函数 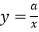 与正比例函数
与正比例函数 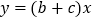 在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )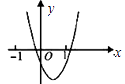
A.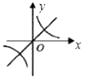
B.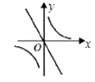
C.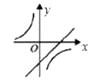
D.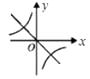
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,
 ,点D在BC所在的直线上,点E在射线AC上,且
,点D在BC所在的直线上,点E在射线AC上,且 ,连接DE.
,连接DE.(1)如图①,若
 ,
,  ,求
,求 的度数;
的度数;(2)如图②,若
 ,
,  ,求
,求 的度数;
的度数;(3)当点D在直线BC上(不与点B、C重合)运动时,试探究
 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.
相关试题

