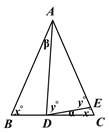
【题目】如图,△ABC中, ![]() ,点D在BC所在的直线上,点E在射线AC上,且
,点D在BC所在的直线上,点E在射线AC上,且![]() ,连接DE.
,连接DE.
(1)如图①,若![]() ,
, ![]() ,求
,求![]() 的度数;
的度数;
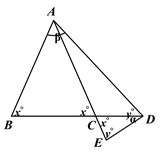
(2)如图②,若![]() ,
, ![]() ,求
,求![]() 的度数;
的度数;
(3)当点D在直线BC上(不与点B、C重合)运动时,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.

参考答案:
【答案】(1)35°(2)30°(3)∠BAD=2∠CDE
【解析】(1).根据∠ACB=∠E+∠CDE=∠E-∠CDE+∠BAD,即可求解;(2).同(1) 的方法可求解;(3).分两种情况讨论:①当点D在点B的左侧时;②当点D在线段BC上时,注意分类讨论的思想.
本题解析:(1)∵∠ACB=∠E+∠CDE, ∠ACB=∠E-∠CDE+∠BAD, ∴∠CDE=35°
(2)![]()
(3)设![]() ,
, ![]() ,
, ![]() ,
,
![]()
①如图1,当点D在点B的左侧时, ![]()
∴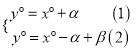 ,
, ![]() 得,
得, ![]() ,∴
,∴![]() `
`
②如图2,当点D在线段BC上时, ![]() ,
,

∴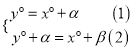 ,
, ![]() 得,
得, ![]() ,∴
,∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定两数a,b之间的一种运算,记作(a,b):如果
 ,那么(a,b)=c.
,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)=_______,(5,1)=_______,(2,
 )=_______.
)=_______.(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用上述这种方法说明下面这个等式成立的理由:(4,5)+(4,6)=(4,30)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AD∥BC,∠ABC=80°,∠BCD=50°,利用平移的知识讨论BC与AD+AB的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC 中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.
(1)如图1,连接CE,
①若CE∥AB,求∠BEC的度数;
②若CE平分∠ACD,求∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.﹣1的平方根是﹣1
B.4的平方根是2
C.如果一个数有平方根,那么这个数的平方根一定有两个
D.任何一个非负数的立方根都是非负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生的艺术特长发展情况,某校音乐组决定围绕“在舞蹈、乐器、声乐、戏曲、其它活动项目中,你最喜欢哪一项活动(每人只限一项)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.

请你根据统计图解答下列问题:
(1)在这次调查中一共抽查了名学生,其中,喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 , 喜欢“戏曲”活动项目的人数是人;
(2)若在“舞蹈、乐器、声乐、戏曲”活动项目任选两项设立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】菱形以特殊的对称美而深受人们的喜爱,在生产生活中有着广泛的应用,小龙家里有一面长4.2m、宽2.8m的墙壁准备装修,现有如图甲所示的型号瓷砖,其形状是一块长30cm、宽20cm的矩形,中间白色部分为菱形,阴影部分为带淡蓝色花纹的全等的四个直角三角形,解答下列各问:

(1)小龙家里的墙壁最少要贴这种瓷砖多少块?
(2)全部贴满后,这面墙壁上有多少个有淡蓝色花纹的菱形?
相关试题

