【题目】在“数学晚会”上,七年级的10个同学藏在10个大盾牌后面,男同学盾牌前面的结果是一个正数,女同学盾牌前面的结果是一个负数,这10个盾牌如图所示,请你通过计算,求出盾牌后面男、女同学各有多少人.

参考答案:
【答案】盾牌后面有4个男同学,6个女同学
【解析】
各项计算得到结果,即可做出判断.
解:(-15)16=1516>0;
5÷(-25)=![]() <0;
<0;
因为任何数的平方是非负数,所以x2≥0,所以x2+1>0;
8÷(7-77)=8÷(-70)=![]() <0;
<0;
1-2-3=-4<0;
-1×|-62|=-1×36=-36<0;
5×(-1)2015=5×(-1)=-5<0;
-[-(+8)]=-(-8)=8>0;
-23+(-32)=-8+(-9)=-17<0;
(-28)3×(-7)5=283×75>0.
则正数有4个,负数有6个,所以盾牌后面有4个男同学,6个女同学.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:数学活动课上,乐老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.
理解:
(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;
(2)如图2,在圆内接四边形ABCD中,AB是⊙O的直径,AC=BD.求证:四边形ABCD是对等四边形;
(3)如图3,在Rt△PBC中,∠PCB=90°,BC=11,tan∠PBC= ,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=4,BC=3,点P从点A出发,以每秒4个单位长度的速度沿折线AC-CB运动,到点B停止.当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB 于点Q,再以PQ为斜边作等腰直角三角形△PQR,且点R与△ABC的另一条直角边始终在PQ同侧,设△PQR与△ABC重叠部分图形的面积为S(平方单位).点P的运动时间为t(秒).
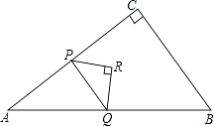
(1)求点P在AC边上时PQ的长,(用含t的代数式表示);
(2)求点R到AC、PQ所在直线的距离相等时t的取值范围;
(3)当点P在AC边上运动时,求S与t之间的函数关系式;
(4)直接写出点R落在△ABC高线上时t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;
Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:

则正确的配对是( )
A. ①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ B. ①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C. ①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ D. ①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ
-
科目: 来源: 题型:
查看答案和解析>>【题目】证明:两条平行线被第三条直线所截,一组同位角的平分线互相平行.

已知:如图,_______________________.
求证:_____________________________.
证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进甲,乙两种商品,若购买6件甲商品和3件乙商品共用108元;若购买5件甲商品和2件乙商品共用88元.
(1)求甲,乙两种商品每件的价格;
(2)已知该商店购买乙商品的件数比购买甲商品的件数多8件,如果需要购买甲,乙两种商品的总件数不少于32件,且商店购买的甲、乙两种商品的总费用不超过292元,那么该商店有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
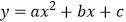 的图象如图所示,反比例函数
的图象如图所示,反比例函数 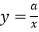 与正比例函数
与正比例函数 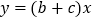 在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )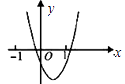
A.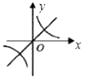
B.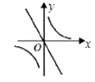
C.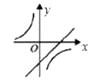
D.
相关试题

