【题目】如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )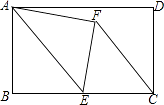
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解:∵BC=12,点E是BC的中点,
∴EC=BE=6,
由翻折变换的性质可知,BE=FE,∠BEA=∠FEA,
∴EF=EC,
∴∠EFC=∠ECF,
∵∠BEA+∠FEA=∠EFC+∠ECF,
∴∠BEA=∠ECF,
∵tan∠BEA= ![]() =
= ![]() ,
,
∴tan∠ECF= ![]() ,
,
所以答案是:B.
【考点精析】解答此题的关键在于理解三角形的外角的相关知识,掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上.则细线的另一端所在位置的点的坐标是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(﹣6,0),B(4,0),C(0,8),把△ABC沿直线BC翻折,点A的对应点为D,抛物线y=ax2﹣10ax+c经过点C,顶点M在直线BC上.
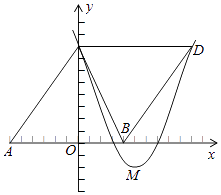
(1)证明四边形ABCD是菱形,并求点D的坐标;
(2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P,使得△PBD与△PCD的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某奶茶店开业大酬宾推出
 四款饮料.1千克A饮料的原料是2千克苹果,3千克梨,1千克西瓜;1千克B饮料的原料是2千克苹果,3千克梨,1千克西瓜;1千克C饮料的原料是3千克苹果,9千克梨,6千克西瓜;1千克D饮料的原料是2千克苹果,6千克梨,4千克西瓜;如果每千克苹果的成本价为2元,每千克梨的成本价为
四款饮料.1千克A饮料的原料是2千克苹果,3千克梨,1千克西瓜;1千克B饮料的原料是2千克苹果,3千克梨,1千克西瓜;1千克C饮料的原料是3千克苹果,9千克梨,6千克西瓜;1千克D饮料的原料是2千克苹果,6千克梨,4千克西瓜;如果每千克苹果的成本价为2元,每千克梨的成本价为 元,每千克西瓜的成本价为
元,每千克西瓜的成本价为 元.开业当天全部售罄,销售后,共计苹果的总成本为100元,并且梨的总成本为126元,那么西瓜的总成本为_____元.
元.开业当天全部售罄,销售后,共计苹果的总成本为100元,并且梨的总成本为126元,那么西瓜的总成本为_____元. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形
 的底边
的底边 长为
长为 ,面积是
,面积是 , 腰
, 腰 的垂直平分线
的垂直平分线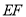 分别交
分别交 边于
边于 点.若点
点.若点 为
为 边的中点,点
边的中点,点 为线段EF上一动点,则
为线段EF上一动点,则 周长的最小值为( )
周长的最小值为( )
A.
 B.
B. C.
C.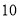 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按图中所标注的数据,计算图中实线所围成的面积S是( )

A.50B.62C.65D.68
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用3辆A型车和2辆B型车载满货物一次可运货17吨;用2辆A型车和3辆B型车载满货物一次可运货l8吨,某物流公刊现有35吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)l辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
相关试题

