【题目】已知![]() 是
是![]() 的平分线,点
的平分线,点![]() 是射线
是射线![]() 上一点,点C、D分别在射线
上一点,点C、D分别在射线![]() 、
、![]() 上,连接PC、PD.
上,连接PC、PD.
(1)发现问题
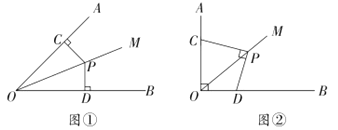
如图①,当![]() ,
,![]() 时,则PC与PD的数量关系是________.
时,则PC与PD的数量关系是________.
(2)探究问题
如图②,点C、D在射线OA、OB上滑动,且∠AOB=90°,∠OCP+∠ODP=180°,当![]() 时,PC与PD在(1)中的数量关系还成立吗?说明理由.
时,PC与PD在(1)中的数量关系还成立吗?说明理由.
参考答案:
【答案】(1)PC=PD;(2)PC=PD仍然成立.理由见解析.
【解析】
(1)根据角平分线的性质可得出PC=PD;
(2)过P分别作PE⊥OB于E,PF⊥OA于F,由角平分线的性质得PE=PF,然后根据同角的补角相等得出∠FCP=∠PDE,即可由AAS证明△CFP≌△DEP,从而得证.
解:(1)∵OM是∠AOB的平分线,PC⊥OA,PD⊥OB,
∴PC=PD,
故答案为:PC=PD;
(2)PC=PD仍然成立.理由如下:
过P分别作PE⊥OB于E,PF⊥OA于F,
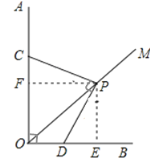
∴∠CFP=∠DEP=90°,
∵OM是∠AOB的平分线,∴PE=PF.
∵∠OCP+∠ODP=180°,又∠ODP+∠PDE=180°,
∴∠OCP=∠PDE,即∠FCP=∠PDE,
在△CFP和△DEP中,
 ,
,
∴△CFP≌△DEP(AAS),
∴PC=PD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子里有红、黄、白三种颜色的球共50个,它们除了颜色不同外都相同,其中黄球的个数比白球的个数少5个,已知从袋子里随机摸出一个球是红球的概率是
 .
.(1)求袋子里红球的个数;
(2)求从袋子里随机摸出一球是白球的概率,说明理由.
-
科目: 来源: 题型:
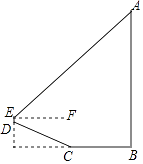
查看答案和解析>>【题目】位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
A.22.5 米
B.24.0 米
C.28.0 米
D.33.3 米 -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b与y=kbx,它们在同一坐标系内的图象可能为 ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式组
 有且只有三个整数解,且关于x的分式方程
有且只有三个整数解,且关于x的分式方程  ﹣
﹣  =﹣1有整数解,则满足条件的整数a的值为( )
=﹣1有整数解,则满足条件的整数a的值为( )
A.15
B.3
C.﹣1
D.﹣15 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)图1中阴影部分面积为______,图2中阴影部分面积为_____,对照两个图形的面积可以验证________公式(填公式名称)请写出这个乘法公式________.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.

相关试题

