【题目】位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)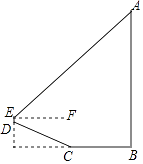
A.22.5 米
B.24.0 米
C.28.0 米
D.33.3 米
参考答案:
【答案】C
【解析】解:过点E作EM⊥AB与点M,
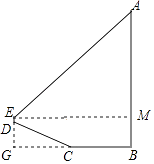
∵斜坡CD的坡度(或坡比)i=1:2.4,BC=CD=13米,
∴设CD=x,则CG=2.4x.
在Rt△CDG中,
∵DG2+CG2=DC2,即x2+(2.4x)2=132,解得x=5,
∴DG=5米,CG=12米,
∴EG=5+0.5=5.5米,BG=13+12=25米.
∵EM⊥AB,AB⊥BG,EG⊥BG,
∴四边形EGBM是矩形,
∴EM=BG=25米,BM=EG=5.5米.
在Rt△AEM中,
∵∠AEM=42°,
∴AM=EMtan42°≈25×0.90=22.5米,
∴AB=AM+BM=22.5+5.5=28米.
所以答案是:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】假设有足够多的黑白围棋子,摆成一个“中”字,下列图形中,第①个图形中有4 枚黑子和4枚白子,第②个图形中有6枚黑子和11枚白子,第③个图形中有8枚黑子和18枚白子,…,按此规律排列,则第⑧个图形中黑子和白子的枚数分别为( )

A.14和48
B.16和48
C.18和53
D.18和67 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,将一块等腰直角三角形的直角顶点放在斜边
,将一块等腰直角三角形的直角顶点放在斜边 的中点
的中点 处,将三角板绕点
处,将三角板绕点 旋转,三角板的两直角边分别交射线
旋转,三角板的两直角边分别交射线 、
、 于
于 、
、 两点.如图①、②、③是旋转三角板得到的图形中的3种情况.
两点.如图①、②、③是旋转三角板得到的图形中的3种情况.(1)观察图①,当三角板绕点
 旋转到
旋转到 时,我们发现:
时,我们发现: __________
__________ .(选填“
.(选填“ ”、“
”、“ ”或“
”或“ ”)
”)(2)当三角板绕点
 旋转到图②所示位置时,判断(1)题中
旋转到图②所示位置时,判断(1)题中 与
与 之间的大小关系还存在吗?请你结合图②说明理由.
之间的大小关系还存在吗?请你结合图②说明理由.(3)三角板绕点
 旋转,
旋转, 是否能成为等腰三角形?若能,指出所有情况(那写出
是否能成为等腰三角形?若能,指出所有情况(那写出 为等腰三角形时
为等腰三角形时 的长);若不能,请说明理由.
的长);若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子里有红、黄、白三种颜色的球共50个,它们除了颜色不同外都相同,其中黄球的个数比白球的个数少5个,已知从袋子里随机摸出一个球是红球的概率是
 .
.(1)求袋子里红球的个数;
(2)求从袋子里随机摸出一球是白球的概率,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b与y=kbx,它们在同一坐标系内的图象可能为 ( )
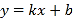
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
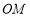 是
是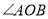 的平分线,点
的平分线,点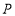 是射线
是射线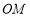 上一点,点C、D分别在射线
上一点,点C、D分别在射线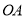 、
、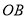 上,连接PC、PD.
上,连接PC、PD.(1)发现问题
如图①,当
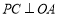 ,
,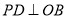 时,则PC与PD的数量关系是________.
时,则PC与PD的数量关系是________.(2)探究问题
如图②,点C、D在射线OA、OB上滑动,且∠AOB=90°,∠OCP+∠ODP=180°,当
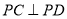 时,PC与PD在(1)中的数量关系还成立吗?说明理由.
时,PC与PD在(1)中的数量关系还成立吗?说明理由.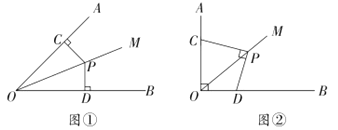
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式组
 有且只有三个整数解,且关于x的分式方程
有且只有三个整数解,且关于x的分式方程  ﹣
﹣  =﹣1有整数解,则满足条件的整数a的值为( )
=﹣1有整数解,则满足条件的整数a的值为( )
A.15
B.3
C.﹣1
D.﹣15
相关试题

