搜索
【题目】一次函数y=kx+b与y=kbx，它们在同一坐标系内的图象可能为 （ ）
参考答案：
【答案】A
【解析】
试题分析：根据一次函数的图象与系数的关系，有由一次函数y=kx+b图象分析可得k、b的符号，进而可得kb的符号，从而判断y=kbx的图象是否正确，即：
A、由一次函数y=kx+b图象可知k＜0，b＞0，即kb＜0；一次函数y=kbx的图象可知kb＜0，两函数解析式均成立；
B、由一次函数y=kx+b图象可知k＜0，b＞0，即kb＜0，与次函数y=kbx的图象可知kb＞0矛盾；
C、由一次函数y=kx+b图象可知k＞0，b＜0，即kb＜0，与次函数y=kbx的图象可知kb＞0矛盾；
D、由一次函数y=kx+b图象可知k＞0，b＞0；即kb＞0，与次函数y=kbx的图象可知kb＜0矛盾．
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=x2﹣4x﹣3的顶点坐标是.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校学生骑自行车从学校去某地植树，过了一段时间学校派后勤人员开车去送树苗和植树工具，学生、后勤人员离开学校的距离y（千米）与行驶时间x（分钟）的函数图象如图所示．
（1）根据图中信息，求学生骑自行车的速度和后勤人员开车的速度；
（2）说出B点的意义并求出B点的坐标；
（3）请你直接写出学生队伍与后勤人员都在运动中相距3千米的时间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M在线段OA和射线AC上运动．
（1）求直线AB的解析式．
（2）求△OAC的面积．
（3）是否存在点M，使△OMC的面积是△OAC的面积的
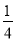？若存在求出此时点M的坐标；若不存在，说明理由．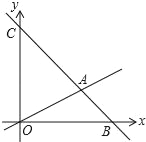
-
科目： 来源： 题型：
查看答案和解析>>【题目】(8分)选择适当的方法解方程：
(1)2(x－3)＝3x(x－3)． (2)2x2－3x＋1＝0．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点M（﹣3，2）关于y轴对称的点的坐标为（ ）
A. （3，2） B. （3，﹣2） C. （﹣3，﹣2） D. （﹣3，2）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝1，与x轴的一个交点坐标为(－1，0)，下列结论：
①4ac＜b2；
②方程ax2＋bx＋c＝0的两个根是x1＝－1，x2＝3；
③3a＋c＞0；
④当y＞0时，x的取值范围是－1≤x＜3 ；
⑤当x＜0时，y随x增大而增大；
其中正确的个数是 ( )
A. 4个 B. 3个 C. 2个 D. 1个
相关试题
