【题目】以矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1),一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】∵矩形的两条对称轴相交于对角线的交点处,即坐标原点是对角线的交点,
∴点C和点A关于原点对称,
∴点C的坐标为(-2,1),
要把抛物线上的一点由点A移到点C,就需要将抛物线向左移动4个单位,再向下移动2个单位,
∴移动后,抛物线的解析式为: ![]() ,即
,即 ![]() .
.
所以答案是:A.
【考点精析】本题主要考查了矩形的性质和坐标与图形变化-平移的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
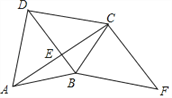
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为线段
为线段 上一点,点
上一点,点 为
为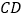 的中点,且
的中点,且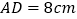 ,
,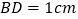
(1)求
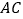 的长
的长(2)若点
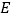 在直线
在直线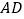 上,且
上,且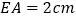 ,求
,求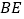 的长
的长
-
科目: 来源: 题型:
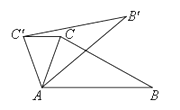
查看答案和解析>>【题目】如图,在
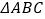 中,∠CAB=70°,在同一平面内, 将
中,∠CAB=70°,在同一平面内, 将 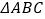 绕点A旋转到
绕点A旋转到 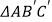 的位置,使得CC′∥AB,则
的位置,使得CC′∥AB,则 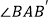 =( )
=( )
A.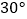
B.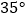
C.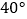
D.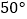
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
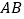 、
、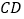 相交于点
相交于点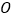 ,
,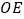 平分
平分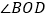 ,
,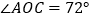 ,
,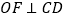
(1)与
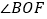 互余的角;
互余的角;(2)求
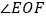 的度数.
的度数.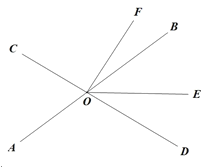
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数
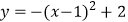 的图象与性质,下列说法正确的是( )
的图象与性质,下列说法正确的是( )
A.对称轴是直线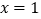 ,最小值是
,最小值是 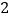
B.对称轴是直线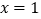 ,最大值是
,最大值是 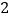
C.对称轴是直线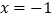 ,最小值是
,最小值是 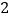
D.对称轴是直线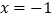 ,最大值是
,最大值是 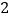
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形组成的5×8方格中,△ABC的顶点都在格点上.
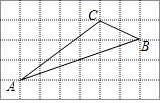
(1)在给定的方格中,以直线AB为对称轴,画出△ABC的轴对称图形△ABD.
(2)求sin∠ABD的值.
相关试题

