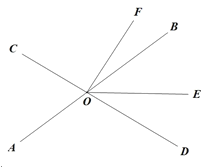
【题目】如图,直线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]()
(1)与![]() 互余的角;
互余的角;
(2)求![]() 的度数.
的度数.
参考答案:
【答案】(1)![]() 或
或![]() ,(2)
,(2)![]()
【解析】
(1)由垂直的定义可得∠BOF+∠BOD=90°,再由∠BOD=∠AOC,可得∠BOF+∠AOC=90°,由此即可得答案;
(2)根据对顶角相等以及垂直的定义可求出∠BOF=90°-72°=18°,再由OE平分∠BOD,得出∠BOE的度数,继而可求得答案.
(1)∵OF⊥CD,
∴∠FOD=90°,
∴∠BOF+∠BOD=90°,
∵∠BOD=∠AOC,
∴∠BOF+∠AOC=90°,
∴与∠BOF互余的角为∠BOD或∠AOC;
(2)∵直线AB和CD相交于点O,
∴∠BOD=∠AOC=72°,
∵OF⊥CD,
∴∠BOF=90°-72°=18°,
∵OE平分∠BOD,
∴∠BOE=![]() ∠BOD=36°,
∠BOD=36°,
∴∠EOF=36°+18°=54°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为线段
为线段 上一点,点
上一点,点 为
为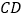 的中点,且
的中点,且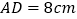 ,
,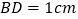
(1)求
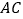 的长
的长(2)若点
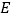 在直线
在直线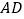 上,且
上,且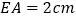 ,求
,求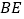 的长
的长
-
科目: 来源: 题型:
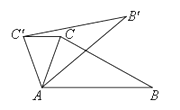
查看答案和解析>>【题目】如图,在
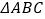 中,∠CAB=70°,在同一平面内, 将
中,∠CAB=70°,在同一平面内, 将 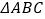 绕点A旋转到
绕点A旋转到 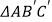 的位置,使得CC′∥AB,则
的位置,使得CC′∥AB,则 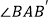 =( )
=( )
A.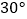
B.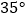
C.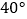
D.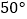
-
科目: 来源: 题型:
查看答案和解析>>【题目】以矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1),一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.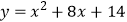
B.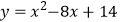
C.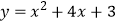
D.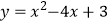
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数
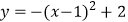 的图象与性质,下列说法正确的是( )
的图象与性质,下列说法正确的是( )
A.对称轴是直线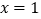 ,最小值是
,最小值是 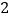
B.对称轴是直线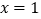 ,最大值是
,最大值是 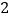
C.对称轴是直线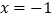 ,最小值是
,最小值是 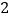
D.对称轴是直线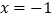 ,最大值是
,最大值是 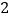
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形组成的5×8方格中,△ABC的顶点都在格点上.
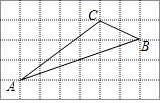
(1)在给定的方格中,以直线AB为对称轴,画出△ABC的轴对称图形△ABD.
(2)求sin∠ABD的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
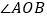 画射线
画射线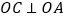 ,射线
,射线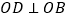 ,试写出
,试写出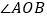 和
和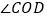 的数量关系,并说明理由.
的数量关系,并说明理由.
相关试题

