【题目】如图,![]() 为线段
为线段![]() 上一点,点
上一点,点![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]()
(1)求![]() 的长
的长
(2)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求
,求![]() 的长
的长
![]()
参考答案:
【答案】(1)6cm,(2)5或9cm.
【解析】
(1)根据线段中点的定义可求得CD的长,再根据线段的和差即可求得AC的长;
(2)分点E在线段BA的延长线上、在线段AB上两种情况分别画图进行讨论即可.
(1)∵点B为CD的中点,BD=1cm,
∴CD=2BD=2cm,
∵AC=AD-BD,AD=8cm,
∴AC=8-2=6cm;
(2)∵点B为CD的中点,BD=1cm,
∴BC=BD=1cm,
①如图1,点E在线段BA的延长线上时,
![]()
BE=AE+AC+CB=2+6+1=9cm;
②如图2,点E在线段BA上时,
![]()
BE=AB-AE=AC+CB-AE=6+1-2=5cm,
综上,BE的长为9cm或5cm.
-
科目: 来源: 题型:
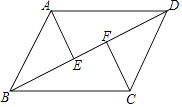
查看答案和解析>>【题目】如图,E,F为平行四边形ABCD的对角线BD上的两点,AE⊥BD于点E,CF⊥BD于点F. 求证:AE=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
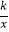 与 y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与 y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A.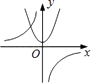
B.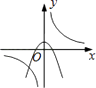
C.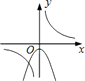
D.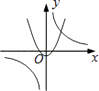
-
科目: 来源: 题型:
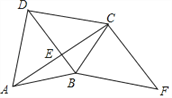
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
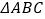 中,∠CAB=70°,在同一平面内, 将
中,∠CAB=70°,在同一平面内, 将 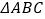 绕点A旋转到
绕点A旋转到 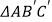 的位置,使得CC′∥AB,则
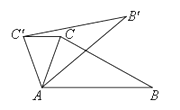
的位置,使得CC′∥AB,则 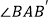 =( )
=( )
A.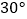
B.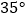
C.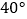
D.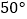
-
科目: 来源: 题型:
查看答案和解析>>【题目】以矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1),一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.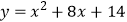
B.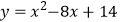
C.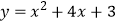
D.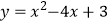
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
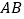 、
、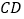 相交于点
相交于点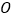 ,
,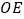 平分
平分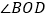 ,
,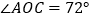 ,
,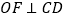
(1)与
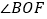 互余的角;
互余的角;(2)求
 的度数.
的度数.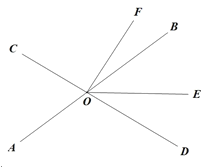
相关试题

