【题目】如图,□ABCD中,对角线AC与AB、AD的夹角分别为α、β,点E是AC上任意一点,给出如下结论:①AB sinα=AD sinβ;②S△ABE=S△ADE;③ADsinα=AB sinβ. 其中正确的个数有( )
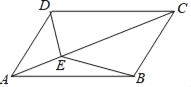
A. 0个 B. 1个 C. 2个 D. 3个
参考答案:
【答案】C
【解析】分析:
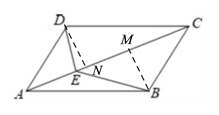
如下图,(1)过点D作DN⊥AC于点N,过点B作BM⊥AC于点M,由此可得DN=AD·sinβ,BM=AB·sinα,由已知条件易证△ABC≌△CDA,从而可得S△ABC=![]() ACAB·sinα=
ACAB·sinα=![]() ACAD·sinβ,由此可得AB· sinα=AD· sinβ,即结论①成立;(2)由S△ABE=
ACAD·sinβ,由此可得AB· sinα=AD· sinβ,即结论①成立;(2)由S△ABE=![]() AEABsinα,S△ADE=
AEABsinα,S△ADE=![]() AEAdsinβ结合(1)中所得AB·sinα=AD·sinβ即可得到S△ABE=S△ADE,故结论②成立;(3)由已知条件易证△ADN≌△CBM,由此可得DN=BM,即AD·sinβ=AB·sinα,AD·sinα=AB·
AEAdsinβ结合(1)中所得AB·sinα=AD·sinβ即可得到S△ABE=S△ADE,故结论②成立;(3)由已知条件易证△ADN≌△CBM,由此可得DN=BM,即AD·sinβ=AB·sinα,AD·sinα=AB·![]() ,由此可知只有当
,由此可知只有当![]() =
=![]() 时,才有ADsinα=ABsinβ成立,故结论③不一定成立;
时,才有ADsinα=ABsinβ成立,故结论③不一定成立;
详解:
由题意,可知∠CAB=α,∠DAC=β,如下图,过点D作DN⊥AC于点N,过点B作BM⊥AC于点M,
∴DN=AD·sinβ,BM=AB·sinα,
(1)∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD.
在△ABC与△CDA中,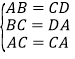 ,
,
∴△ABC≌△CDA,
∴S△ABC=S△CDA,
∵S△ABC=![]() ACABsinα,S△CDA=
ACABsinα,S△CDA=![]() ACADsinβ,
ACADsinβ,
∴AB·sinα=AD·sinβ,①正确;
(2)∵S△ABE=![]() AEABsinα,S△ADE=
AEABsinα,S△ADE=![]() AEADsinβ,且AB·sinα=AD·sinβ,
AEADsinβ,且AB·sinα=AD·sinβ,
∴S△ABE=S△ADE,②正确;
(3)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAN=∠BCM,
又∵∠DNA=∠BMC=90°,
∴△ADN≌△CBM,
∴DN=BM,
∴AD·sinβ=AB·sinα,
∴AD·sinα=AB·![]() ,
,
由此可知只有当![]() =
=![]() 时,才有ADsinα=AB sinβ成立,故结论③不一定成立;
时,才有ADsinα=AB sinβ成立,故结论③不一定成立;
综上所述,3个结论中,只有①②成立.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知 a b , a 与b 两个数在数轴上对应的点分别为点 A 、点 B ,求 A 、 B 两点之间的距离.
(探索)
小明利用绝对值的概念,结合数轴,进行探索:

(1)补全小明的探索
(应用)
(2)若点C 对应的数c ,数轴上点C 到A、B 两点的距离相等,求c .(用含a、b 的代数式表示)
(3)若点 D对应的数 d ,数轴上点 D 到 A 的距离是点 D 到 B 的距离的nn 0 倍,请探索 n 的取值范围与点 D 个数的关系,并直接写出a、b 、d、n 的关系.
-
科目: 来源: 题型:
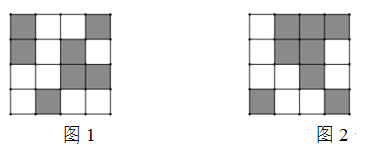
查看答案和解析>>【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式a×23-b×22-c×21+d计算出每一行的数据.第一行表示年级,第二行表示班级,如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的编号是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初中各年级学生每天的平均睡眠时间(单位:h,精确到1 h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
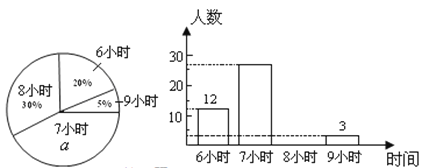
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数
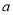 的值为_______,所抽查的学生人数为______;
的值为_______,所抽查的学生人数为______;(2)求出平均睡眠时间为8小时的人数,并补全条形图;
(3)求出这部分学生的平均睡眠时间的平均数;
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明过程:
如图,AB∥CD,AD∥BC,BE平分∠ABC,DF平分∠ADC.
求证:BE∥DF.

证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.( )
又∵AD∥BC,(已知)
∴ +∠C=180°.( )
∴∠ABC=∠ADC.( )
∵BE平分∠ABC,(已知)
∴∠1=
 ∠ABC.( )
∠ABC.( )同理,∠2=
 ∠ADC.
∠ADC.∴ =∠2.
∵AD∥BC,(已知)
∴∠2=∠3.( )
∴∠1=∠3,
∴BE∥DF.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了调查学生书写规范汉字的能力,从七年级1000名学生中随机抽选了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整)
组别
成绩x分
频数(人数)
第1组
x<60
4
第2组
60≤x<70
a
第3组
70≤x<80
20
第4组
80≤x<90
b
第5组
90≤x<100
10

请结合图表完成下列各题
(1)填空:表中a的值为_______,b的值为_______,扇形统计图中表示第1组所对应的圆心角度数为_______.
(2)若测试成绩不低于80分为优秀,请你估计从该校七年级学生中随机抽查一个学生,他是规范汉字书写优秀的概率是_______;
(3)若测试成绩在60~80分之间(含60分,不含80分)为合格,请你估计则该校七年级学生规范汉字书写不合格的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批进价为10元的新商品,为寻求合适的销售价格,他们进行了4天的试销,试销情况如下表:
第1天
第2天
第3天
第4天
日销售单价x(元)
20
30
40
50
日销售量y(个)
300
200
150
120
(1)根据试销情况,请你猜测并求出y与x之间的函数关系式;
(2)若该商场计划每天销售这种商品的利润要达到3600元,问该商品销售单价应定为多少元?
相关试题

