【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式a×23-b×22-c×21+d计算出每一行的数据.第一行表示年级,第二行表示班级,如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的编号是_______.
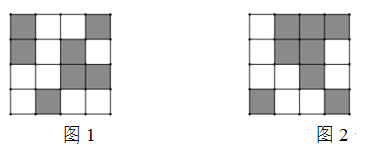
参考答案:
【答案】070629.
【解析】
利用公式求出图2中每行表示的数据,将其组合起来即可得出结论.
解:由图2可知:第一行数字从左往右依次是0,1,1,1,则表示的数据为0×23+1×22+1×21+1=7,计作07,
第二行数字从左往右依次是0,1,1,0,则表示的数据为0×23+1×22+1×21=6,计作06,
第三行数字从左往右依次是0,0,1,0,则表示的数据为0×23+0×22+1×21=2,计作2,
第四行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作9.
∴图2代表的统一学号为070629.
故答案为:070629.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和爸爸周末到湿地公园进行锻炼,两人同时从家出发,匀速骑共享单车到达公园入口,然后一同匀速步行到达驿站,到达驿站后小明的爸爸立即又骑共享单车按照来时骑行速度原路返回,在公园入口处改为步行,并按来时步行速度原路回家,小明到达驿站后逗留了10分钟之后骑车回家,爸爸在锻炼过程中离出发地的路程与出发的时间的函数关系如图.
(1)图中m=_____,n=_____;(直接写出结果)
(2)小明若要在爸爸到家之前赶上,问小明回家骑行速度至少是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程(组)
(1)2(x﹣1)3+16=0.
(2)
 ;
;(3)
 .
. (4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知 a b , a 与b 两个数在数轴上对应的点分别为点 A 、点 B ,求 A 、 B 两点之间的距离.
(探索)
小明利用绝对值的概念,结合数轴,进行探索:

(1)补全小明的探索
(应用)
(2)若点C 对应的数c ,数轴上点C 到A、B 两点的距离相等,求c .(用含a、b 的代数式表示)
(3)若点 D对应的数 d ,数轴上点 D 到 A 的距离是点 D 到 B 的距离的nn 0 倍,请探索 n 的取值范围与点 D 个数的关系,并直接写出a、b 、d、n 的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初中各年级学生每天的平均睡眠时间(单位:h,精确到1 h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
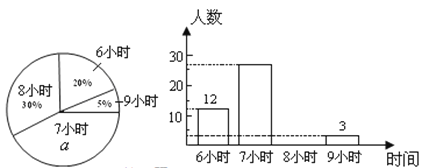
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数
 的值为_______,所抽查的学生人数为______;
的值为_______,所抽查的学生人数为______;(2)求出平均睡眠时间为8小时的人数,并补全条形图;
(3)求出这部分学生的平均睡眠时间的平均数;
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD中,对角线AC与AB、AD的夹角分别为α、β,点E是AC上任意一点,给出如下结论:①AB sinα=AD sinβ;②S△ABE=S△ADE;③ADsinα=AB sinβ. 其中正确的个数有( )
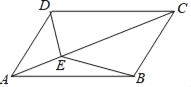
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明过程:
如图,AB∥CD,AD∥BC,BE平分∠ABC,DF平分∠ADC.
求证:BE∥DF.

证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.( )
又∵AD∥BC,(已知)
∴ +∠C=180°.( )
∴∠ABC=∠ADC.( )
∵BE平分∠ABC,(已知)
∴∠1=
 ∠ABC.( )
∠ABC.( )同理,∠2=
 ∠ADC.
∠ADC.∴ =∠2.
∵AD∥BC,(已知)
∴∠2=∠3.( )
∴∠1=∠3,
∴BE∥DF.( )
相关试题

