Question

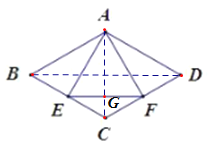
【题目】如图，在菱形中，分别是边中点，则面积等于（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

连接AC，BD，AC交EF于点G．由菱形的性质可判断△ABC和△ADC都是等边三角形，根据中位线的性质可证AC⊥EF，在Rt△CEG中求出CG、EG的长，然后根据三角形的面积公式可求S△AEG=，即可求解．

连接AC，BD，AC交EF于点G．

∵四边形ABCD是菱形，∠BAD=120°，

∴AC⊥BD，∠ABC=∠ADC=60°，

∴△ABC和△ADC都是等边三角形，

∴∠ACB=∠ACD=60°，

∵E、F分别是BC、CD的中点，

∴CE=CF=2，EF//BD，

∴AC⊥EF，

∴∠CEG=∠CFG=30°，

∴CG=1，

∴EG=，AG=4-1=3，

∴S△AEG=，

同理可求S△AFG=，

∴面积等于+=．

故选A．