【题目】认真阅读下面的材料,完成有关问题:
材料 在学习绝对值时,老师教过我们绝对值的几何含义,如|5-3|表示5,3在数轴上对应的两点之间的距离;|5+3|=|5-(-3)|,所以|5+3|表示5,-3在数轴上对应的两点之间的距离;|5|=|5-0|,所以|5|表示5在数轴上对应的点到原点的距离.一般地,点A,B在数轴上分别表示有理数a,b,那么A,B之间的距离可表示为|a-b|.
(1)点A,B,C在数轴上分别表示有理数-5,-1, 3,那么A到B的距离是 ,A到C的距离是_____.(直接填最后结果)
(2)点A,B,C在数轴上分别表示有理数x,-2,1,那么A到B的距离与A到C的距离之和可表示为 (用含绝对值的式子表示).
(3)利用数轴探究:
①设|x-3|+|x+1|=p,当x的值取在不小于-1 且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是_____;
②求|x|+|x-2|的最小值以及此时x的取值范围?
参考答案:
【答案】(1)4,8; (2)|x+2|+|x-1|或|x-(-2)|+|x-1|;(3)①4;②当x的取值在不小于0且不大于2的范围时,|x|+|x-2|的最小值是2.
【解析】
(1)根据两点间距离公式代入相应的值即可得出答案;
(2)根据两点间距离公式分别求出A到B的距离和A到C的距离,两式相加即可得出答案;
(3)①根据“x的值取在不小于-1 且不大于3的范围”将绝对值化简再进行计算即可得出答案;②根据①中的探究可知,当x的取值在不小于0且不大于2的范围时,|x|+|x-2|有最小值,再根据x的取值范围化简绝对值,即可得出最小值.
解:(1)A到B的距离是:![]() ;
;
A到C的距离是:![]() ;
;
(2)A到B的距离是:![]() ;
;
A到C的距离是:![]()
∴A到B的距离与A到C的距离之和可表示为:![]() ;
;
(3)①∵x的值取在不小于-1 且不大于3的范围
∴![]()
又|x-3|+|x+1|=p
∴p=4,这个最小值是4;
②∵当x的值取在不小于-1 且不大于3的范围时,|x-3|+|x+1|有最小值,最小值为4
∴当x的取值在不小于0且不大于2的范围时,|x|+|x-2|有最小值,最小值为2.
-
科目: 来源: 题型:
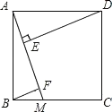
查看答案和解析>>【题目】如图,正方形 ABCD 的边长为 5,点 M 是边 BC 上的点,DE⊥AM 于点 E,BF∥DE,交 AM 于点 F.若E 是 AF 的中点,则 DE 的长为( )
A.
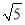 B.2
B.2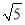 C.4D.
C.4D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1至图3是将正方体截去一部分后得到的几何体.

(1)根据要求填写表格:
面数/f
顶点数/v
棱数/e
图1
_____
_____
____
图2
_____
_____
_____
图3
___
_____
____
(2)猜想f,v,e三个数量间的关系.
(3)根据猜想计算,若一个几何体的顶点有2 019个,棱有4 035条,试求出它的面数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】均匀的正四面体的各面依次标有
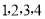 四个数字
四个数字 小明做了60次投掷试验,结果统计如下:
小明做了60次投掷试验,结果统计如下: 朝下数字
1
2
3
4
出现的次数
16
20
14
10
 计算上述试验中“4朝下”的频率是多少?
计算上述试验中“4朝下”的频率是多少? “根据试验结果,投掷一次正四面体,出现2朝下的概率是
“根据试验结果,投掷一次正四面体,出现2朝下的概率是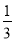 ”的说法正确吗?为什么?
”的说法正确吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,七年级某班男同学进行了100米测验,达标成绩为15秒,下表是梦想小组8名男生的成绩记录,其中“+”表示成绩大于15秒.
﹣0.8
+1
﹣1.2
0
﹣0.7
+0.6
﹣0.4
﹣0.1
问:(1)这个小组男生的达标率为多少?(达标率=
 )
)(2)这个小组男生的平均成绩是多少秒?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形 ABCD 中,点 G 是 AD 的中点,GE⊥CG 交 AB 于 E,BE=BC,连接 CE 交 BG 于 F,则∠BFC 等于_______.
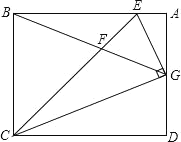
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中只装有2个白色围棋子和1个黑色围棋子,围棋子除颜色外其余均相同.从这个盒子中随机地摸出1个围棋子,记下颜色后放回,搅匀后再随机地摸出1个围棋子记下颜色.请用画树状图(或列表)的方法,求两次摸出的围棋子颜色都是白色的概率.
相关试题

